Time Complexity

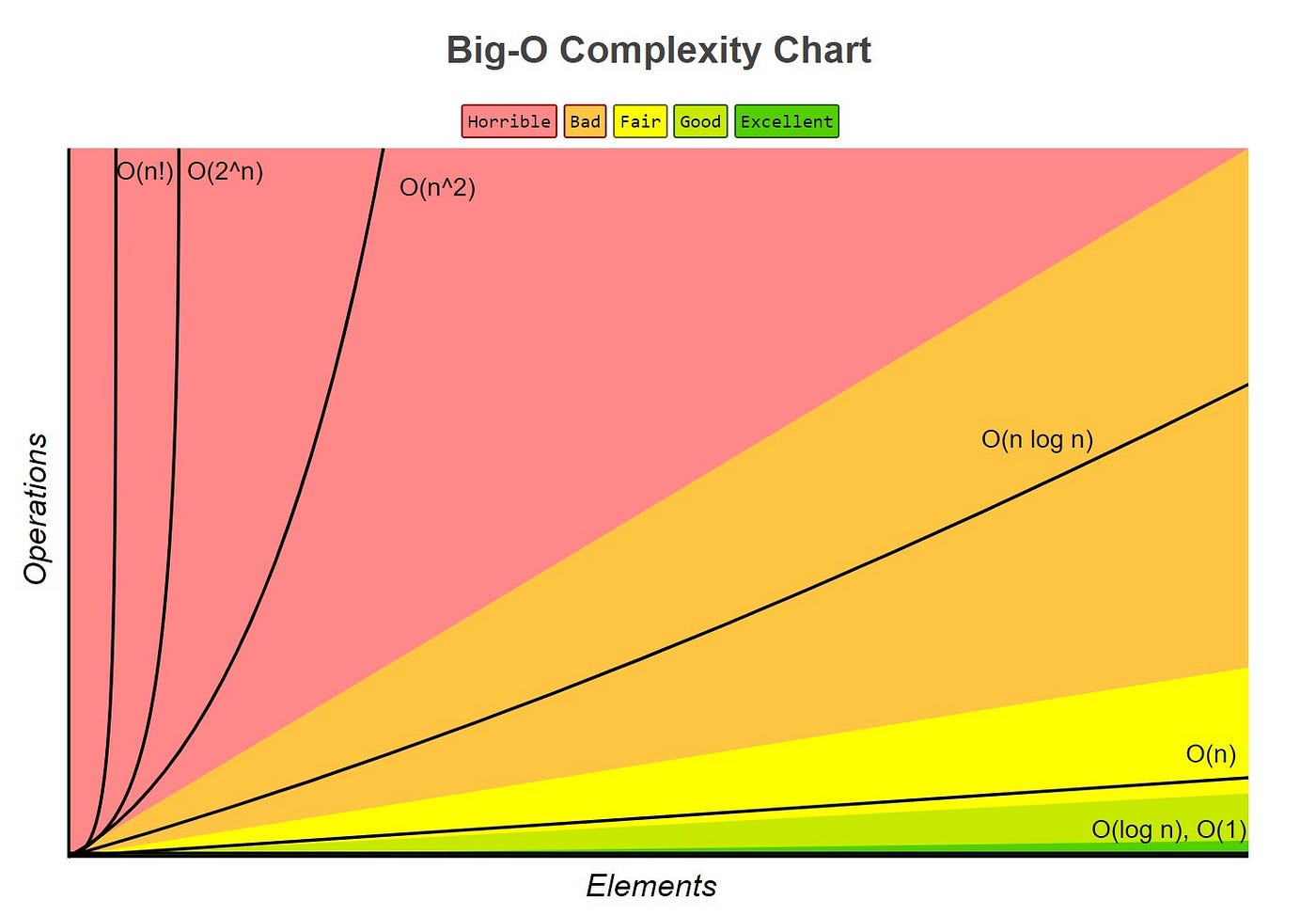
Big-O ($O$)

Definition

• f(n) = $O$(g(n)) iff $\exists$ c, n₀ > 0 such that f(n)$\le$ c $\cdot$ g(n) $\forall$ n $\ge$ n₀

Examples

• 3n+2 = $O$(n)

  When c=4, n₀ = 2, 3n+2 $\le$ 4n for all n $\ge$ 2.

• 100n+6 = $O$(n)

  When c=101, n₀ = 6, 100n+6 $\le$ 101n for all n $\ge$ 6.

• 10n²+4n+2 = $O$(n²)

  When c=11, n₀ = 5, 10n²+4n+2 $\le$ 11n² for all n $\ge$ 5.

• Properties

  • f(n) = $O$(g(n)) states that $O$(g(n)) is an upper bound of f(n), so n = $O$(n) = $O$(n^2.5) = $O$(n³) = $O$(nⁿ). However, we want g(n) as small as possible .
  • Big-O refers to worst-case running time of a program.

Big-Omega($\Omega$)

Definition

• f(n) = $\Omega$(g(n)) iff $\exists$ c, n₀ > 0 such that f(n)$\ge$ c $\cdot$ g(n) $\forall$ n $\ge$ n₀ .

Examples

• 3n+2 = $\Omega$(n)

  When c=3, n₀ = 1, 3n+2 $\ge$ 3n $\forall$ n $\ge$ 1.

• 100n+6 = $\Omega$(n)

  When c=100, n₀ = 1, 100n+6 $\ge$ 100n $\forall$ n $\ge$ 1.

• 10n²+4n+2 = $\Omega$(n²)

  When c=1, n₀ = 1, 10n²+4n+2 $\ge$ n² $\forall$ n $\ge$ 1.

Properties

• f(n) = $\Omega$(g(n)) states that $\Omega$(g(n)) is a lower bound of f(n).
• $\Omega$ refers to best-case running time of a program.

Big-Theta($\theta$)

Definition

• f(n) = $\theta$(g(n)) iff f(n) = $O$(g(n)) and f(n) = $\Omega$(g(n)).

Examples

• 3n+2 = $\theta$(n)
• 100n+6 = $\theta$(n)
• 10n²+4n+2 = $\theta$(n²)

Properties

• f(n) = $\theta$(g(n)) states that $\theta$(g(n)) is a tight bound of f(n).
• $\theta$ refers to average-case running time of a program.

Cheat Sheets

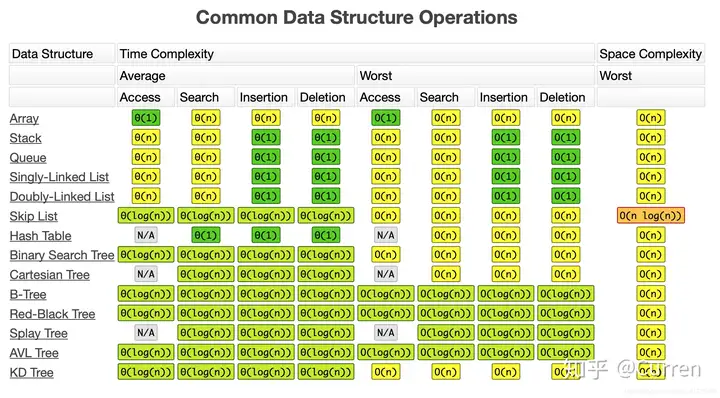
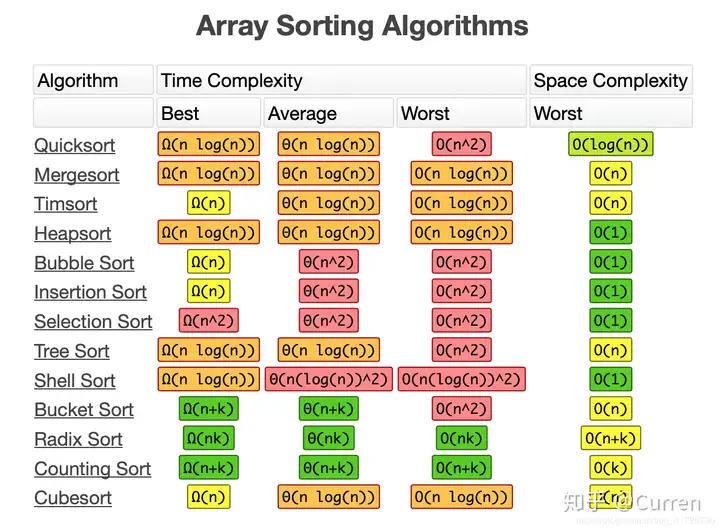
參考資料

• Big-O Algorithm Complexity Cheat Sheet