Compiler 筆記 (3)

參考 清華大學 李政崑老師 編譯器設計講義

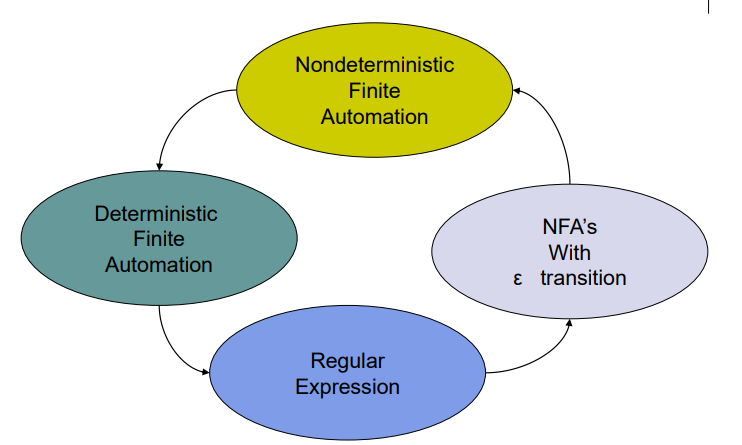
Regular Expression

• A Language is a set of strings that can be formed from the given alphabet
• Grammar defines a Language

Example 1

• a | b denotes {a, b}
• (a | b)(a | b) denotes {ab, aa, ba, bb}
• a* = {$\epsilon$, a, aa, aaa, …}
• a$^+$ = {a, aa, aaa, …}
• (a | b) = {a, b}
• a | a* b = {a, b, ab, aab, aaab, …}

Example 2

(11 + 0)_ (00 + 1)_

不能奇數個 1 出現在奇數個 0 前面，像是 01010 就不可能

Example 3

(1 + 01 + 001)_ ($\epsilon$ + 0 + 00)_

不能連續三個 0，像是 000

Example 4

(D*.D | D.D*)

D = [0 ~ 9]
0.5, .5, 123.6, 9.2, 9.237, 9.

Finite State Automata (FSA)

• FSA is a 5-tuple (Q, $\Sigma$, $\delta$, $q_0$, F)
• Q is a set of states
• $\Sigma$ is an input alphabet, symbol
• $\delta$ is a transition function
• $q_0$ is the initial state
• F is a set of final states

Example

Vending Machine

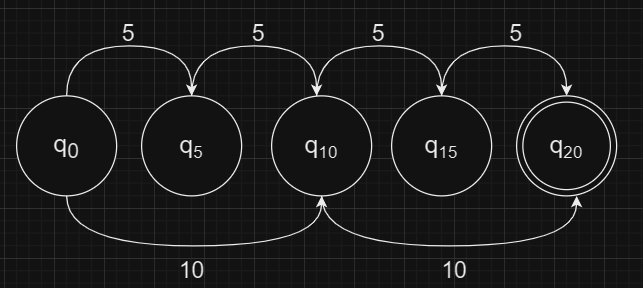
• M = (Q, $\Sigma$, $\delta$, $q_{0}$, F)
• Q = {$q_{0}, q_{5}, q_{10}, q_{15}, q_{20}$}
• $\Sigma$ = {5, 10}
• F = {$q_{20}$}
• $\delta$($q_{0}$, 5) = $q_{5}$, $\delta$($q_{5}$, 5) = $q_{10}$
• $\delta$($q_{10}$, 5) = $q_{15}$, $\delta$($q_{15}$, 5) = $q_{20}$
• $\delta$($q_{0}$, 10) = $q_{10}$, $\delta$($q_{10}$, 10) = $q_{20}$

NFA (non-deterministic Finite State Automata)

• 可能有多個 Next State
• NFA with empty string move ($\epsilon$)
  • $\epsilon$ 允許到新狀態的變換不消耗任何輸入符號。例如，如果它處於狀態 1，下一個輸入符號是 a，它可以移動到狀態 2 而不消耗任何輸入符號，因此就有了歧義：在消耗字母 a 之前系統是處於狀態 1 還是狀態 2 呢 ? 由於這種歧義性，可以更加方便的談論系統可以處在的可能狀態的集合。因此在消耗字母 a 之前，NFA-ε 可以處於集合 {1,2} 內的狀態中的任何一個。等價的說，你可以想像這個 NFA 同時處於狀態 1 和狀態 2: 這給出了對冪集構造的非正式提示：等價於這個 NFA 的 DFA 被定義為此時處於狀態 q={1,2} 中
    • 非確定有限狀態自動機
• NFA without empty string move

DFA (Deterministic Finite State Automata)

• 只有一個 Next State

Example of NFA

$\epsilon$ and $\phi$

• $\epsilon$ is a 0 length string
• $\phi$ is a null, i.e. no string.

r = $\epsilon$

• You can insert any number of epsilons between two alphabets of input string
• Ex: aeeeeeeeeeb, it won’t make any difference
• If we want to denote a null move, I.e.. one state going to other state without any input symbol, then epsilon is used
  • What is the difference between epsilon and phi in Automata?

r = $\phi$

• Denotes empty i.e. no input string exists.

Conversion of NFA without $\epsilon$-transition to DFA

• Every DFA is an NFA, but not vice versa

• There is an equivalent DFA for every NFA

• M = (Q, $\Sigma$, $\delta$, $q_0$, F)

• M’ = (Q’, $\Sigma$, $\delta$’, $q_0’$, F’)

  • Q’ = $2^Q$
  • The state of M’ are all the subset of the set of states of M
  • F’ is the set of all states in Q’ constructing a final states of M
  • $\delta$’([$q_1$, $q_2$, …, $q_i$], a) = [$p_1$, $p_2$, …, $p_j$] iff $\delta$({$q_1$, $q_2$, …, $q_i$}, a) = {$p_1$, $p_2$, …, $p_j$}
  • Note: $2^Q$ is Power Set, meaning that the set of all subsets of Q
    • Q = {a, b, c}
    • $2^Q$ = {$\phi$, {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c}}

• Conversion of NFA to DFA (Example 2)

Convert NFA with $\epsilon$-transition to NFA without $\epsilon$-transition

• $\delta$’(q, a) = $\epsilon$-closure($\delta$($\epsilon$-closure (q), a))

$\epsilon$-closure

• The set of states that can be reachable by making $\epsilon$-transitions from a given set of start states is called a $\epsilon$-closure

Epsilon-closure Example

• $\epsilon$-closure($q_0$) = {$q_0, q_1, q_2, q_4, q_7$}
• $\epsilon$-closure($q_1$) = {$q_1, q_2, q_4$}
• $\epsilon$-closure($q_2$) = {$q_2$}
• $\epsilon$-closure($q_3$) = {$q_1, q_2, q_3, q_4, q_6, q_7$}
• $\epsilon$-closure($q_4$) = {$q_4$}
• $\epsilon$-closure($q_5$) = {$q_1, q_2, q_3, q_4, q_5, q_6, q_7$}
• $\epsilon$-closure($q_6$) = {$q_1, q_2, q_4, q_6, q_7$}
• $\epsilon$-closure($q_7$) = {$q_7$}
• $\epsilon$-closure($q_8$) = {$q_8$}
• $\epsilon$-closure($q_9$) = {$q_9$}
• $\epsilon$-closure($q_10$) = {$q_10$}

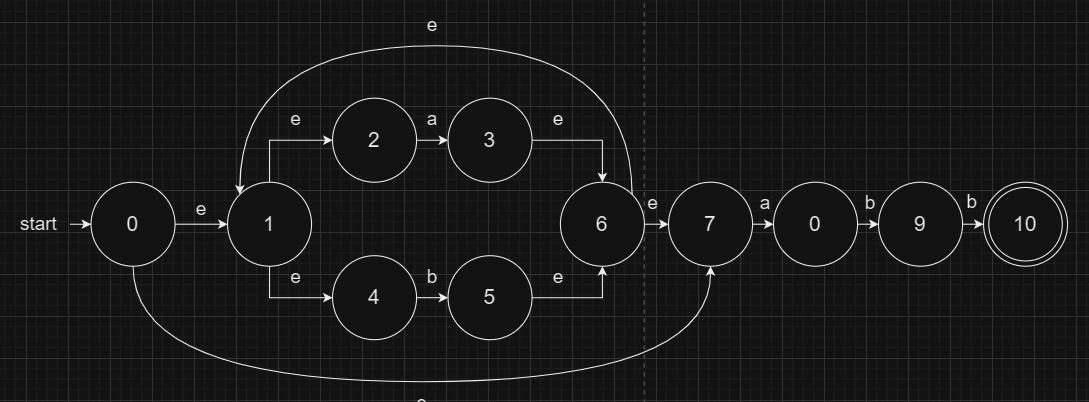
Conversion Example

• $\epsilon$-closure($q_0$) = {$q_0, q_1, q_2$}
• $\delta$($q_0$, 0) = $\epsilon$-closure($\delta$($\epsilon$-closure($q_0$), 0))

$$
\begin{align}
\epsilon\text{-closure}(q_0) &= {q_0, q_1, q_2} \newline
\delta(q_0, 0) &= \epsilon\text{-closure}(\delta(\epsilon\text{-closure}(q_0), 0)) \newline
&= \epsilon\text{-closure}(\delta({q_0, q_1, q_2}, 0)) \newline
&= \epsilon\text{-closure}({q_0}) \newline
&= {q_0, q_1, q_2}
\end{align}
$$

• 對每個 State 都做一次上面的操作

Minimizing the number of states of a DFA

• 一開始把 Final states 和不是 Final states 的 state 分成兩組
  • ex: {A, B, C}, {D, E}
• 每次比較同組的兩個 state，比較所有 inpts 的 next state 是否在同組，不同的話就分開
  • ex: A 輸入 a 變成 C (C 在第一組)、B 輸入 a 變成 D (D 在第二組)，C 和 D 在上一次操作中位於不同組別，所以要把 A、B 分成不同組，變成 {A, C}, {B}, {D, E}
  • 接著就持續比 AC、DE
• 持續執行上述操作，直到沒有改變

Minimization of DFA (Example 1)

其它

Relation

• Reflexive
  if (a, b) /belongs R for every a /belongs A
  aRa

• Symmetry
  aRb = bRa

• transitinity
  aRb, bRc -> aRc

Back tracking is not that powerful
Parsar with no back tracking
(frist set, follow set, selection set)

Ambiguous Grammar

會考的

• bindings
• First class object
  • 可以 assign 到 variable
  • AMP
  • lambda
• call-by-reference, call-by-name, call-by-text, call-by-need (lazy binding)

Finite State Machine vs Push Down Automata

FSM

• $M = (Q, \Sigma, \delta, g_0, F)$
• $\delta(q_0, a) = q_2$

PDA

• $M = (Q, \Sigma, \Gamma, \delta, q_0, Z_0, F)$
  • $Z_0$: initial
  • $\Gamma$: all the state of symbols
• $\delta(q_0, Z_a, a) = q_1$, (push, pop, e)

Example 2

丟進 stack
b
b
b
a
a
a

丟進 c 消光 b
丟進 d 消光 a