數學筆記
我的數學好爛,忘光光,小補一下
泰勒展開式
出發點:希望能夠用多項式來近似任何函數,包含 $sin(x)$、$cos(x)$、$e^x$ 等等,這樣就可以用微積分的方法來解決問題。
$$
f(x) = f(a) + f’(a)(x-a) + \frac{f’’(a)}{2!}(x-a)^2 + \frac{f’’’(a)}{3!}(x-a)^3 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + R_n(x)
$$
其中 $R_n(x)$ 是餘項
推導
$$
f(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + \cdots + a_nx^n
$$
以 $x = 0$ 為例,當兩邊微分 $n$ 次後,得到通式 $a_n$:
$$
f^{(n)}(0) = n! \cdot a_n \Rightarrow a_n = \frac{f^{(n)}(0)}{n!}
$$
把 $a_n$ 代入 $f(x)$ 得到 馬克勞林級數 (Maclaurin Series) :
$$
f(x) = f(0) + \frac{f’(0)}{1!}x + \frac{f’’(0)}{2!}x^2 + \frac{f’’’(0)}{3!}x^3 + \cdots + \frac{f^{(n)}(0)}{n!}x^n
$$
現在為了適用於任意點 $a$,以函數平移的角度來看,從 $x = 0$ 平移到 $x = a$,就是 $x - a$,得到 泰勒展開式 (Taylor Series) :
$$
f(x) = f(a) + \frac{f’(a)}{1!}(x-a) + \frac{f’’(a)}{2!}(x-a)^2 + \frac{f’’’(a)}{3!}(x-a)^3 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n
$$
可以看到,泰勒展開式 是在 $x = a$ 的點展開,馬克勞林級數 是在 $x = 0$ 的點展開,泰勒展開式 是 馬克勞林級數 的一般化。
例子
$e^x$
在 $x = a$ 展開:
$$
e^x = e^a + e^a(x-a) + \frac{e^a}{2!}(x-a)^2 + \frac{e^a}{3!}(x-a)^3 + \cdots + \frac{e^a}{n!}(x-a)^n = \sum_{n=0}^{\infty} \frac{e^a}{n!}(x-a)^n
$$
在 $x = 0$ 展開:
$$
e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots + \frac{x^n}{n!} = \sum_{n=0}^{\infty} \frac{x^n}{n!}
$$
$sin(x)$
在 $x = 0$ 展開:
$$
sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots = \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n+1}}{(2n+1)!}
$$
$cos(x)$
在 $x = 0$ 展開:
$$
cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots = \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n}}{(2n)!}
$$
參考資料
Lagrange Multipliers
用來解決 帶約束條件的最佳化問題。當一個函數的極值問題受到其他等式約束時,可以用 Lagrange Multipliers 來解決。
Level Curves
圖中的紫色平面會把藍色函式 $f(x, y) = 3x - x^3 -2y^2 + y^4$ 切成不同的等高線,每條等高線代表著相同的函數值。綠色的點為紫色平面上的某一點,可以發現這個點不管在哪裡,其算出的梯度向量 $\nabla f$ 永遠與等高線的切線向量垂直。
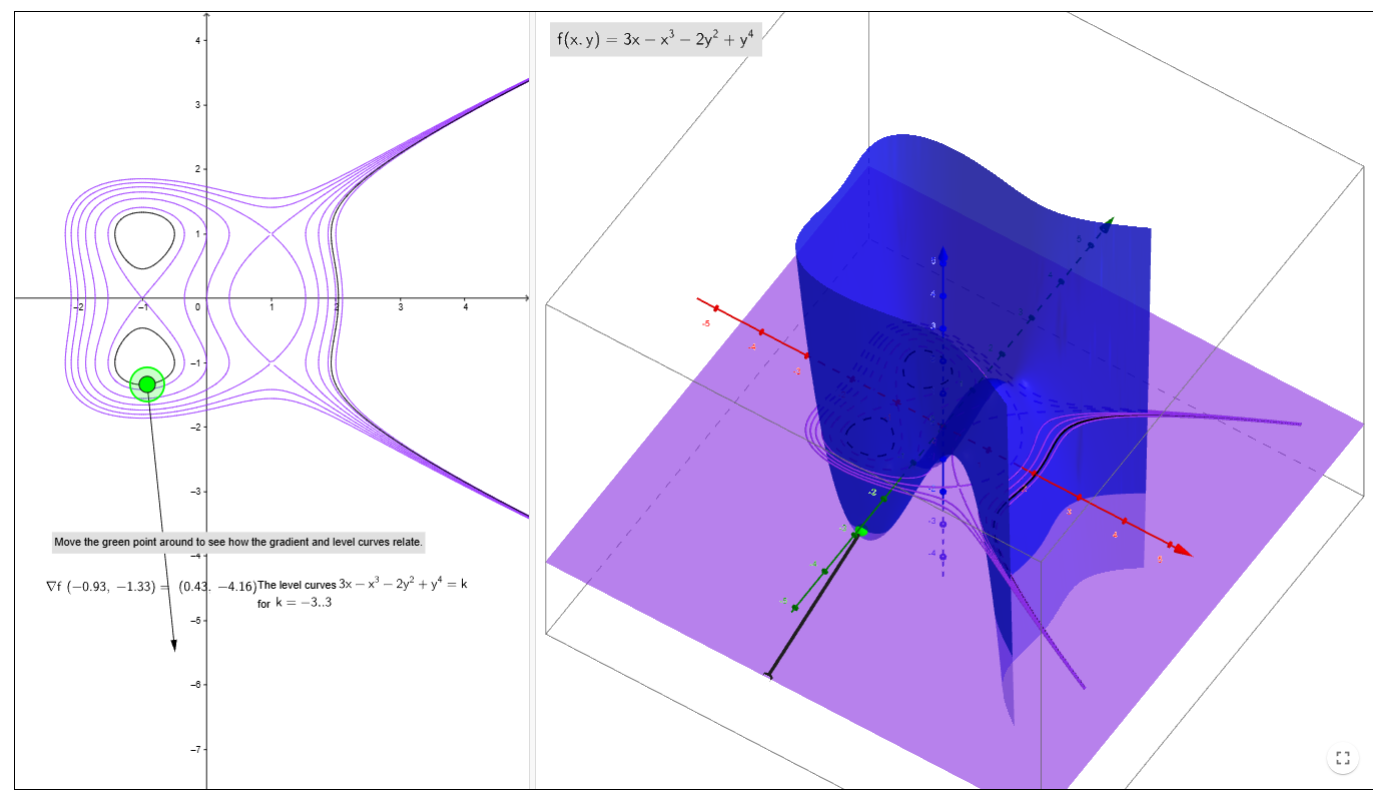
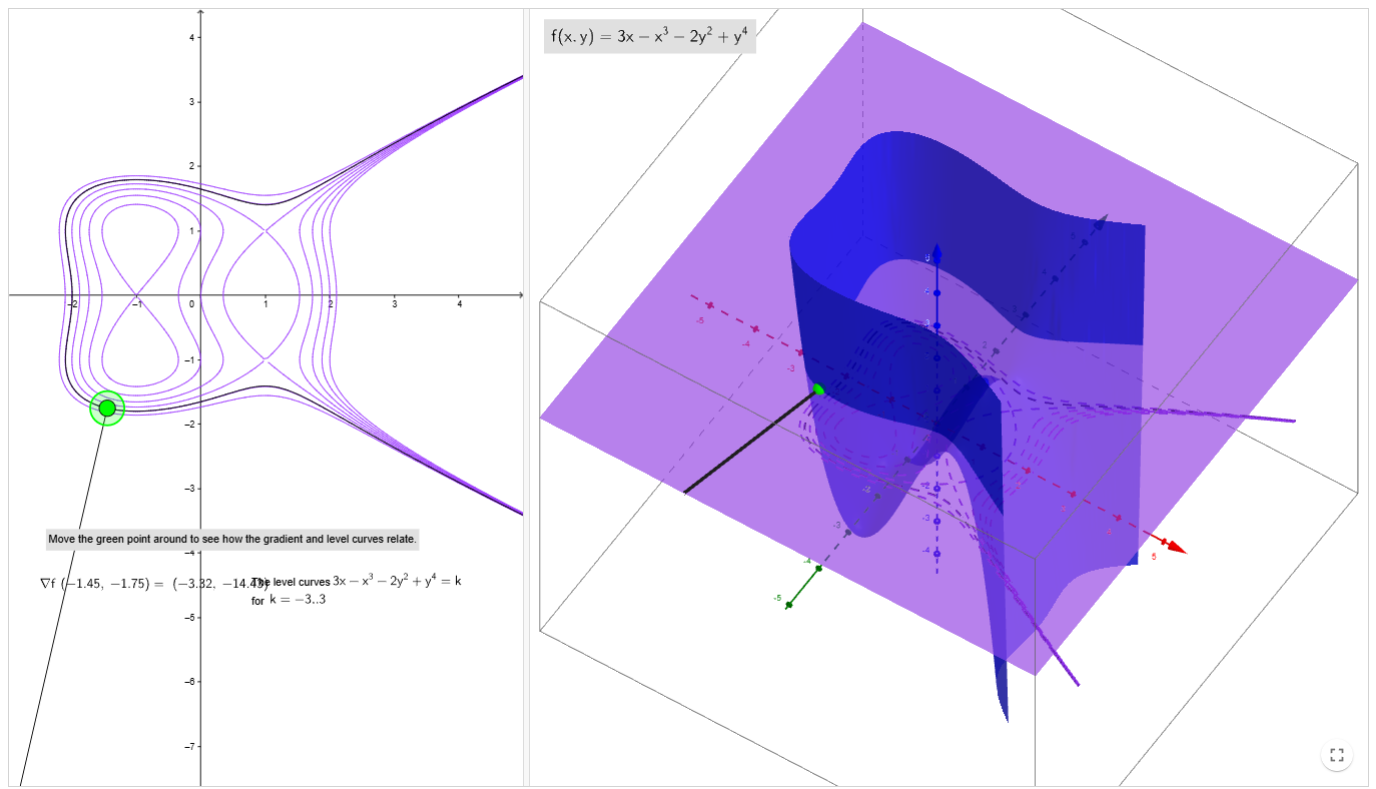
有限制的最佳化問題
在這個圖中,綠色為紅色函式的等高線投影,藍色函式為 $x$、$y$ 的限制條件,橘色函式為紅色函式在限制條件下的函式。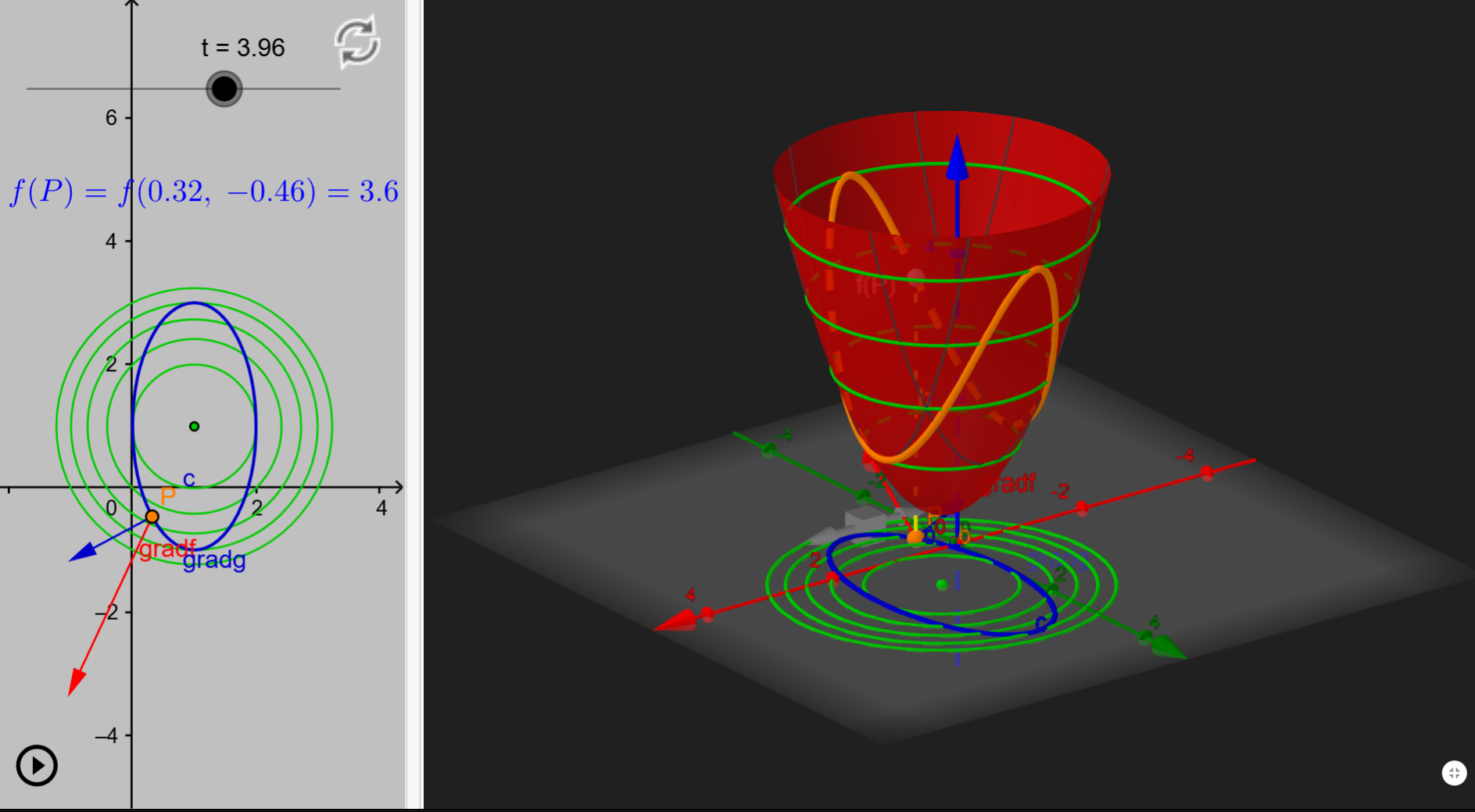
可以發現當極值發生時,等高線的的 Gradient 和限制條件的 Gradient 會平行
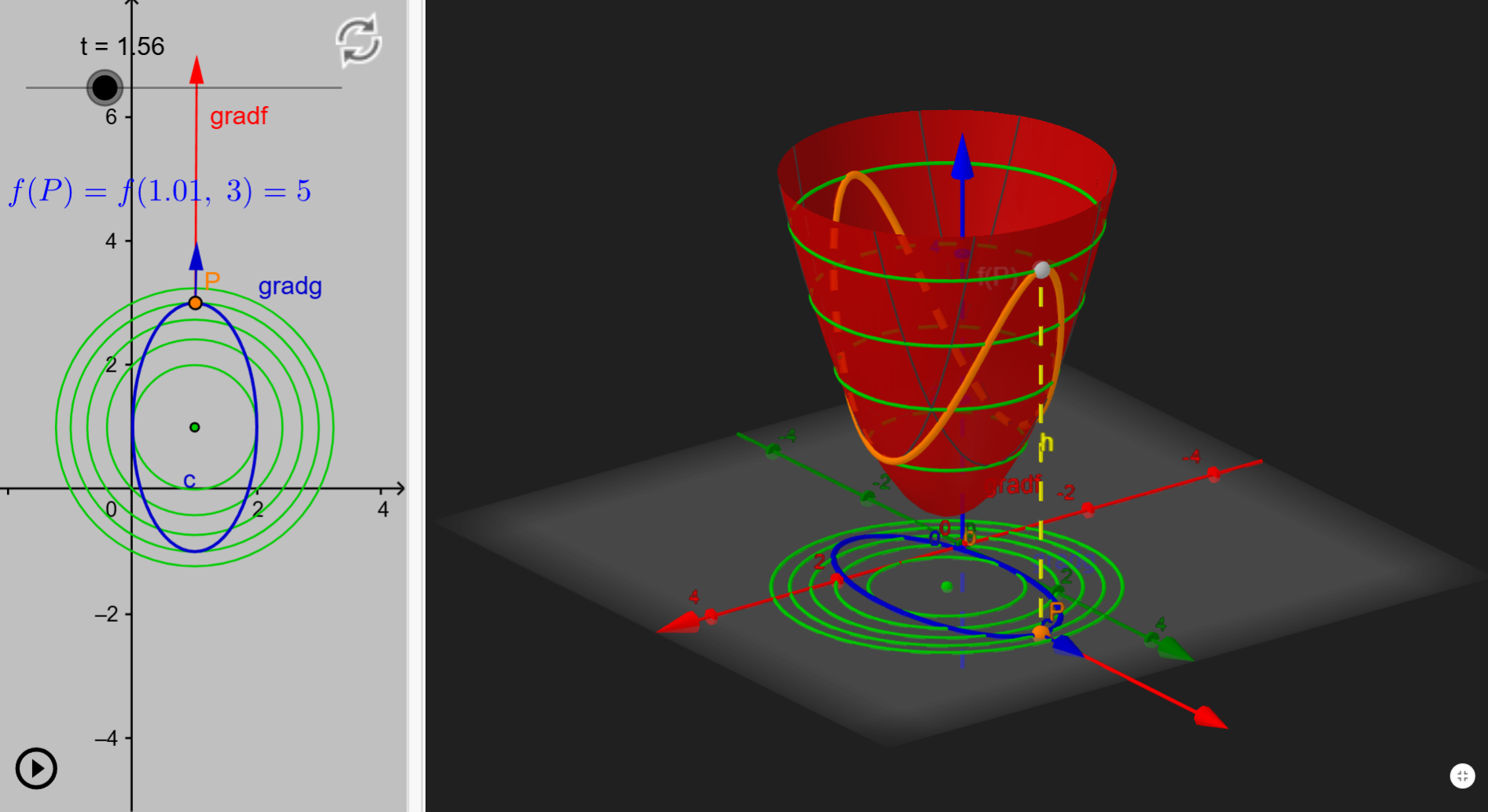
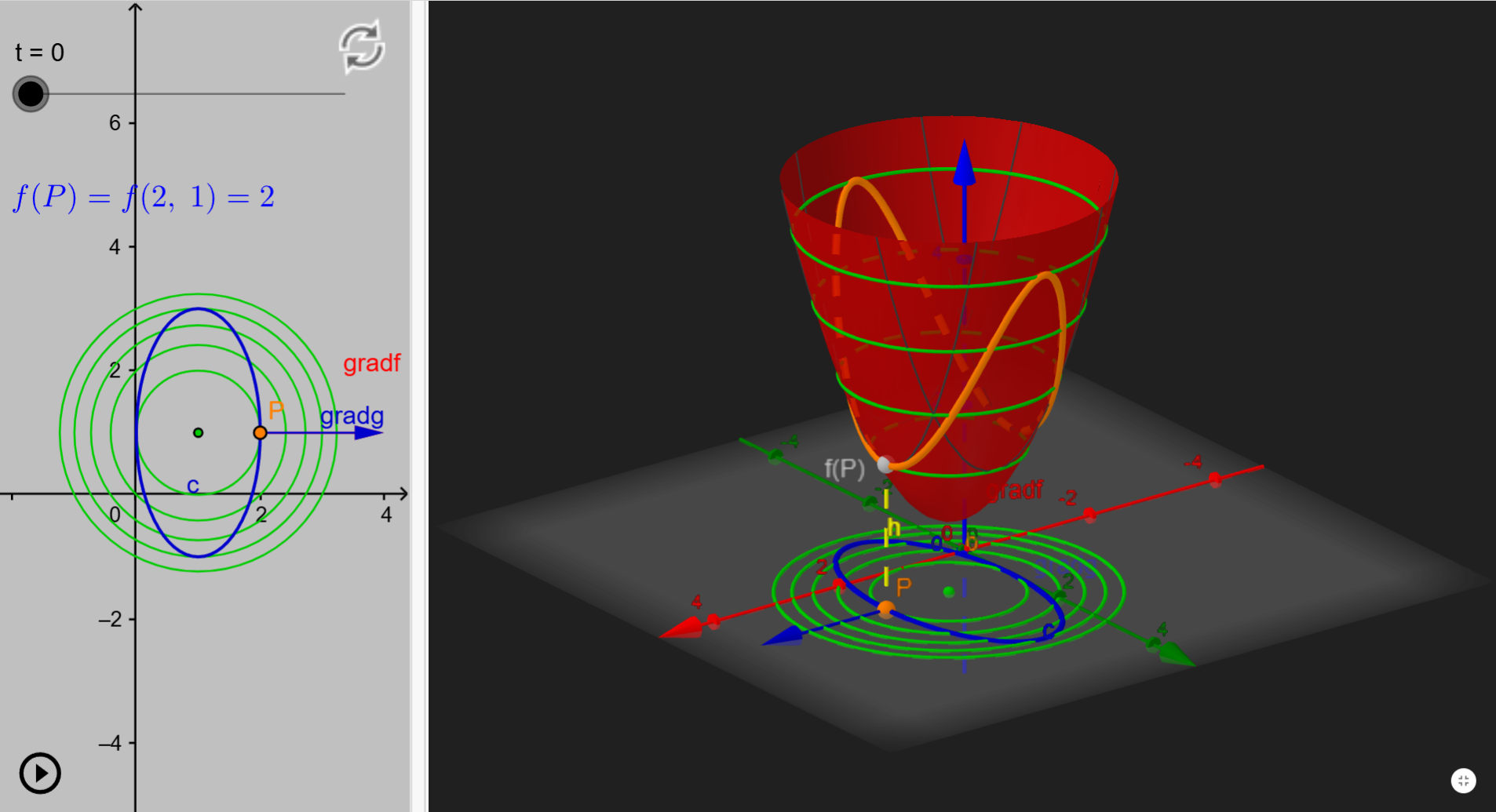
因此可以得到
$$
\nabla f(x, y) = \lambda \nabla g(x, y)
$$
其中 $\lambda$ 就是 Lagrange Multipliers
Example
求 $f(x, y) = x^2 + 2y^2$ 在 $g(x, y) = x^2 + y^2 = 1$ 的極值。
已知:
$$
\begin{aligned}
f(x, y) &= x^2 + 2y^2 \newline
g(x, y) &= x^2 + y^2 = 1 \newline
\end{aligned}
$$
Gradient:
$$
\begin{aligned}
\nabla f(x, y) &= \begin{bmatrix} 2x \ 4y \end{bmatrix} \newline
\nabla g(x, y) &= \begin{bmatrix} 2x \ 2y \end{bmatrix} \newline\newline
\nabla f(x, y) &= \lambda \nabla g(x, y) \newline
\Rightarrow \begin{bmatrix} 2x \ 4y \end{bmatrix} &= \lambda \begin{bmatrix} 2x \ 2y \end{bmatrix} \newline
\end{aligned}
$$
得到
$$
\begin{aligned}
2x &= \lambda 2x \Rightarrow (\lambda-1)x=0 \Rightarrow \begin{cases} x=0 \Rightarrow y^2=1 \Rightarrow y=\pm 1\newline \lambda=1 \end{cases} \newline
&\Rightarrow (x, y) = (0, 1) \text{ or } (0, -1)
\end{aligned}
$$
$$
\begin{aligned}
4y &= \lambda 2y \Rightarrow (\lambda-2)y=0 \Rightarrow \begin{cases} y=0 \Rightarrow x^2=1 \Rightarrow x=\pm 1\newline \lambda=2 \end{cases} \newline
&\Rightarrow (x, y) = (1, 0) \text{ or } (-1, 0)
\end{aligned}
$$
最後把所有 case 代入 $f(x, y)$ 就可以得到極值
Langrange Function
同樣的邏輯,可以整理出更系統化的 Langrange Function:
$$
L(x, y, \lambda) = f(x, y) - \lambda \cdot g(x, y)
$$
且
$$
\frac{\partial L}{\partial x} = 0 ,\quad
\frac{\partial L}{\partial y} = 0 ,\quad
\frac{\partial L}{\partial \lambda} = 0
$$
Example
剛剛的題目,求 $f(x, y) = x^2 + 2y^2$ 在 $g(x, y) = x^2 + y^2 = 1$ 的極值,可以變成:
$$
\begin{aligned}
L(x, y, \lambda) &= f(x, y) - \lambda \cdot g(x, y) \newline
&= x^2 + 2y^2 - \lambda(x^2 + y^2 - 1) \newline
\end{aligned}
$$
$$
\begin{aligned}
\frac{\partial L}{\partial x} &= 2x-2\lambda x =0 \Rightarrow (1 - \lambda)x = 0 \Rightarrow \lambda = 1 \text{ or } x=0\newline
\frac{\partial L}{\partial y} &= 4y-2\lambda y =0 \Rightarrow (2 - \lambda)y = 0 \Rightarrow \lambda = 2 \text{ or } y=0\newline
\frac{\partial L}{\partial \lambda} &= -(x^2 + y^2 - 1) = 0 \Rightarrow x^2 + y^2 = 1
\end{aligned}
$$
得到
$$
\begin{aligned}
\lambda = 1 &\Rightarrow y = 0 \Rightarrow x = \pm 1 \newline
\Rightarrow (x, y) &= (1, 0) \text{ or } (-1, 0) \newline \newline
\lambda = 2 &\Rightarrow x = 0 \Rightarrow y = \pm 1 \newline
\Rightarrow (x, y) &= (0, 1) \text{ or } (0, -1)
\end{aligned}
$$
最後一樣把所有 case 代入 $f(x, y)$ 就可以得到極值