VLSI PDA - Partitioning

參考清大王廷基老師課程講義

Partitioning

把整個設計拆分成較小的電路或系統，每個部分可以獨立設計，最後再合併在一起。Decomposition 必須最小化這蠍子系統間的 Interconnection。其他還要考慮的點有

  • Constraints
    確保每個部分都符合劃定的條件，像是你每個子系統都要用一個 FPGA 來實現，就要確保子系統的元件數量、I/O Pin 的數量不超過 FPGA 的限制

  • Communication
    子系統之間的連線訊號不要出現在 Critical Path 上，晶片內的 Timing 跟 PCB 的 Timing 不一樣

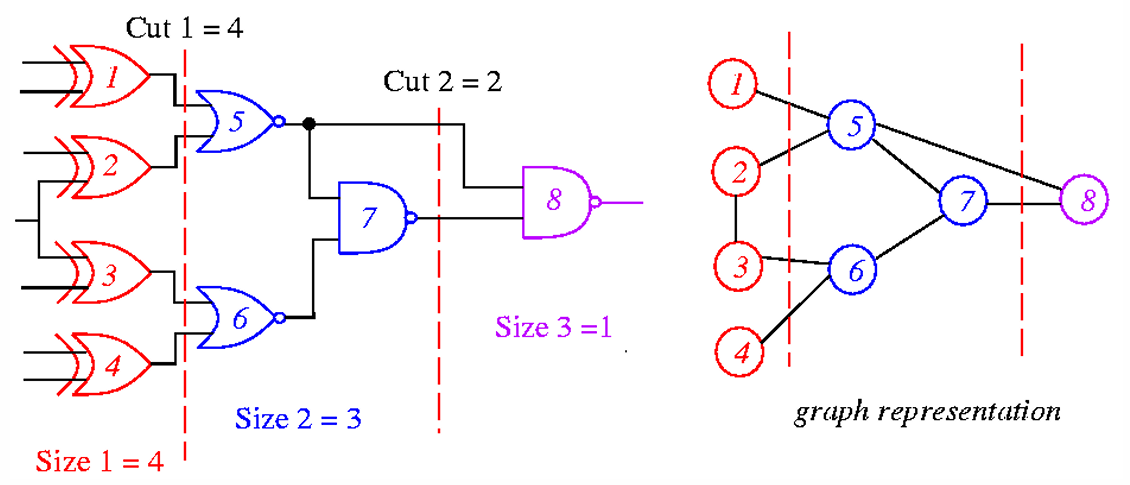
Partitioning

  • Cutset: 一個 Cut 包含很多被切掉的 Net，Cutset 就是這些 Net 的集合
  • Cut size: Cutset 的大小
  • 有些 Edge 可以賦予 Weight (像是 Critical Path 上的 Edge)

Problem

給定 Graph $G = (V, E)$，每個 Vertex $v \in V$ 有 Size $s(v)$，每個 Edge $e \in E$ 有 Weight $w(e)$，要把 set $V$ 分成 $k$ 個 Partition，使得每個 Partition 的 Size 在某限制範圍內，並且最小化 Cutset 的 Weight。

就算是在 $k = 2$、每個頂點 size 都一樣、每條邊的 weight 也一樣的情況下，在有 Size Constraint 的情況下，這個問題還是 NP-Hard

若沒有 Size Constraint，這個問題就是 Maximum Flow Minimum Cut 問題，可以在 Polynomial Time 解決

Kernighan-Lin (KL) Algorithm

KL Algorithm 是一種 Greedy 的 Heuristic Algorithm，不保證找到最佳解，但是通常結果不錯

針對 2-way Partitioning、每個頂點 Size 一樣、每條邊都是 2-terminal nets 的情況，且兩個集合的 Size 要一樣大 (又稱 Balanced Partitioning、Bi-sectioning)

  1. 隨機把所有頂點分成兩個集合 $A$、$B$
  2. Pass
    1. 選出 Gain 最大的 Pair $(u, v)$，$u \in A$、$v \in B$，並且交換 $u$、$v$ 的 Partition
    2. Lock $u$、$v$，之後交換不再考慮這兩個頂點
    3. 直到所有頂點都被 Lock
    4. 算出最大的 Partial Sum Gain $G$，這個 Gain 就是這次 Pass 的 Gain
    5. 假設前 $k$ 個 Pair 的 Gain 總和 $G_k$ 是最大的，就真的去交換前 $k$ 個 Pair
  3. 重複 Pass，直到 Partial Sum Gain $G \leq 0$
  • Gain
    $$
    \text{Gain}(u, v) = \text{Old_Cutset}(A, B) - \text{New_Cutset}(A, B)
    $$
    在同個 Pass 中，第二次算 Gain 的時候，它的 $\text{Old_Cutset}(A, B)$ 是第一次算 Gain 的結果

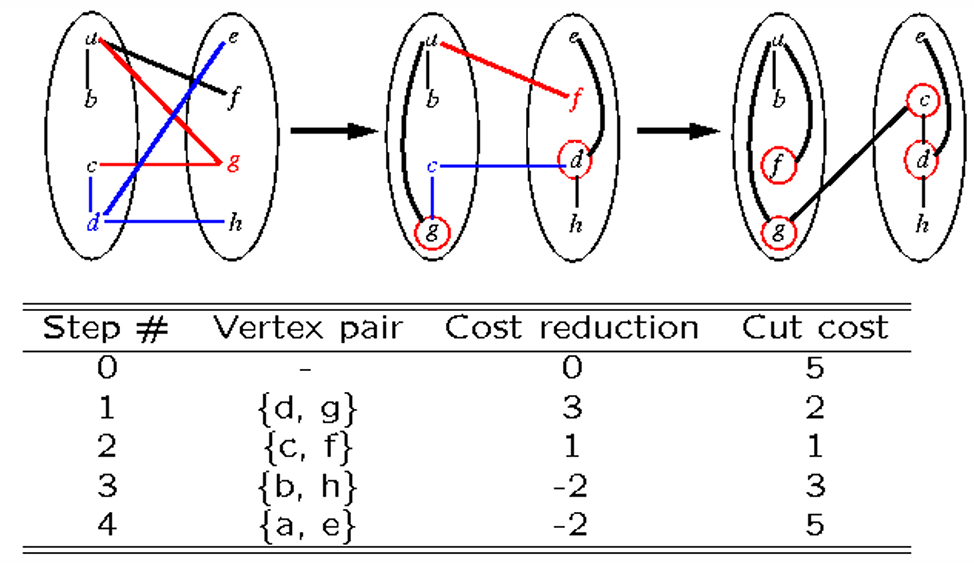
KL Algorithm Example

可以發現交換頂點 $u$、$v$ 之後，$u \in A$、$v \in B$，原本 $u$ 和集合 $B$ 所有頂點的連線都不用算在 Cut ($u$、$v$ 連線除外)，但原本 $u$ 和集合 $A$ 所有頂點的連線都要多算，同理於 $v$。因此在計算的時候只要考慮 External Cost 和 Internal Cost 就好

  • External Cost

    $$
    \text{External_Cost}(u) = \sum_{v \in B} w(u, v)
    $$

  • Internal Cost

    $$
    \text{Internal_Cost}(u) = \sum_{v \in A} w(u, v)
    $$

  • Cost Reduction for moving $u$ (D-value)

    $$
    \text{D-value}(u) = \text{External_Cost}(u) - \text{Internal_Cost}(u)
    $$

  • Cost Reduction for swapping $u$ and $v$ (Gain)
    $$
    \text{Gain}(u, v) = \text{D-value}(u) + \text{D-value}(v) - 2w(u, v)
    $$

假設上述的 $u$、$v$ 是第一次交換，且 $x \in A - {u}$ 會在第二次被交換。第一次交換後必須更新 $x$ 的 D-value，因為 $x$ 的 Internal Cost 和 External Cost 都可能改變。

原本 $x$ 和 $u$ 的連線不用算在 Cut，但是 $x$ 和 $v$ 的連線要算在 Cut，交換後一來一回都各自差兩倍

$$
\text{D-value}^\prime(x) = \text{D-value}(x) + 2w(x, u) - 2w(x, v)
$$

Time Complexity

  • 算出每個頂點的 D-value: $O(n^2)$
  • 一次 Pass 中，要交換所有頂點，每次交換都要找到所有 Pair 中最大的 Gain: $O(n \cdot n^2) = O(n^3)$
  • 若總共有 $r$ 次 Pass: $O(r \cdot n^3)$

要做幾次 Pass 跟 Initial Partition 有關，但不管要做幾次，最後這個演算法一定可以結束，$r$ 一定是 Finite Number

對於 K-way Partitioning 的問題，也可以用 KL Algorithm 來做

  • 一開始 Partition 成 K 個 set，讓這些 set 彼此之間套用 KL Algorithm，直到所有 set 都不再改變
  • 一開始 Partition 成 2 個 set，用 Recursive 的方式來做，直到 Partition 成 K 個 set，一樣兩兩套用 KL Algorithm

KL Algorithm 的缺點

  • 假設所有頂點的 Size 都一樣

    對於真實的 Logic Gate 來說，每個 Gate 的 Size (面積、大小) 都不一樣。

    可以把這個頂點變成很多個單位頂點，形成一個 Clique，兩兩之間都有 Edge 相連，且讓他們的 Weight 超大，在做 KL 的時候可以保證這些頂點會在同一個 Partition。

    但是這樣整個 Graph 的 Size 會變很大，頂點數量和邊數都大幅增加

  • KL Algorithm 只能考慮集合的 Size 相同的情況

    要處理 Unbalanced Partitioning 的問題的話可以加入一些 Dummy Vertices

  • KL Algorithm 不能處理 Hypergraph

    Hypergraph 是一種 Graph 的延伸，一個 Edge 可以連接多個 Vertex。要處裡這種問題要先把 Hypergraph 轉換成一般的 Graph

  • 複雜度高: $O(n^3)$

Fiduccia-Mattheyses (FM) Algorithm

FM Algorithm 一樣是 Greedy 的 Heuristic Algorithm，為 KL Algorithm 的改良版，可以把 Pass 的複雜度降到 Linear Time

與 KL Algorithm 不同的地方

  • 一次只搬運一個 Vertex

    可以想像一次只搬運一個 Vertex 的 Solutuon Space 會更大，更有機會找到更好的解

  • Vertex 可以有不同的 Size

  • 可以處理不嚴格的 Unbalanced Partitioning

  • 用 Bucket Sort 來選擇要移動的 Vertex

  • 每次 Pass 的時間複雜度是 $O(P)$，$P$ 是 Pin 的數量

Notation

  • $n(i)$: Net $i$ 連到 Cell 的數量，ex: $n(1) = 4$
  • $s(i)$: Cell $i$ 的 Size
  • $p(i)$: Cell $i$ 的 Pin 的數量，ex: $p(6) = 3$
  • $C$: Cell 的總數，ex: $C = 6$
  • $N$: Net 的總數，ex: $N = 6$
  • $P$: Pin 的總數，ex: $P = p(1) + p(2) + \cdots + p(C)$

FM Algorithm Example

Cut

Cut

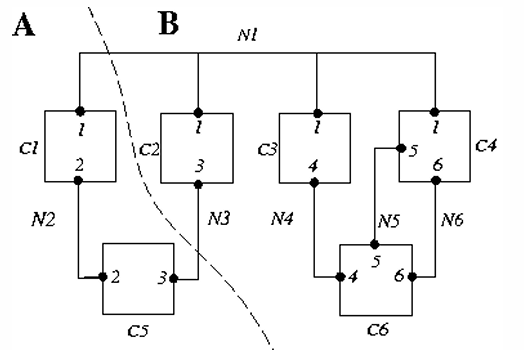
  • Cutstate: 這個 Net 有沒有被切到
    • Net 1 和 Net 3 的狀態是 Cut
    • Net 2、Net 4、Net 5 和 Net 6 的狀態是 Uncut
  • Cutset: 被切到的 Net 的集合
    • Cutset = {Net 1, Net 3}
  • $\lvert A \rvert$ = size of set $A$ = $s(1) + s(5)$
  • $\lvert B \rvert$ = $s(2) + s(3) + s(4) + s(6)$

本質上是一個 Balanced Partitioning 的問題加上一點彈性。給定一個常數 $r$，把一個 Hypergraph Partition 成兩個集合 $A$、$B$ 後，要滿足

$$
\frac{\lvert A \rvert}{\lvert A \rvert + \lvert B \rvert} \approx r
$$

也就是 分在 A 那邊的面積 要佔整個面積的 $r$，且希望 Cutset 的 Size 越小越好

其中 $r$ 的意義是

$$
rW - S_{\text{max}} \leq \lvert A \rvert \leq rW + S_{\text{max}}
$$

其中

  • $W$ 是整個 Hypergraph 的總面積，$W = \lvert A \rvert + \lvert B \rvert$
  • $S_{\text{max}}$ 是最大的 Cell 的 Size

Input Data Structure

根據傳進來的 Netlist，可以建立 Cell Array 和 Net Array，分別需要 $O(P)$ (Pin 數量) 的時間複雜度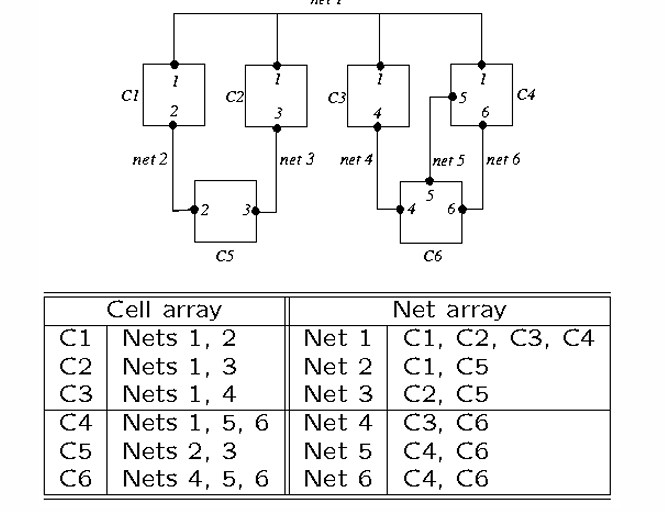
Input Data Structure

Balance & Movement

  • Initial Balance

    先讓 A 為空集合，B 為所有 Cell 的集合，老師提供兩種方法：一種是把 B 按照 Size 做排序，一個一個 Cell 放進 A，直到滿足 $r$ 的條件；另一種是不排序，隨機挑選 Cell 放進 A，直到滿足 $r$ 的條件

  • Gain

    $$
    \text{Gain}(i) = \text{Cutset}(A, B) - \text{Cutset}(A - {i}, B \cup {i})
    $$

    也就是把 Cell $i$ 從 A 搬到 B，Cutset 的 Size 會變小多少

  • Movement

    每次只搬一個 Cell，兩邊之中選一個 Gain 最大的 Cell 搬過去，如果符合 $r$ 的條件就搬，不符合就不搬，並且 Lock 這個 Cell，之後不再考慮 (沒搬成功的不要 Lock)

    最後跟 KL 一樣，直到所有 Cell 都被 Lock 之後，找出最大的 Partial Sum Gain，這個 Gain 就是這次 Pass 的 Gain，真的去搬那些 Cell

Cell Gains and Data Structure Manipulation

首先要知道的是，每個 Cell 移動的 Gain 值跟它的 Pin 數量有關

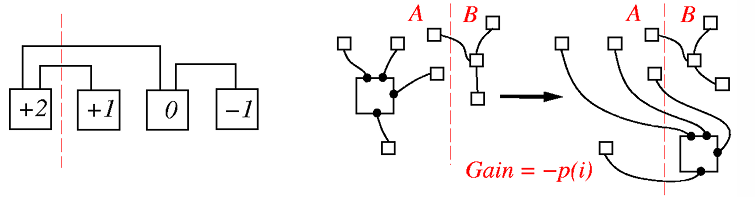
Cell Gains

因此可以確定移動一個 Cell 的 Gain 絕對不會超出它本身 Pin 的數量

$$
-p(i) \leq \text{Gain}(i) \leq p(i)
$$

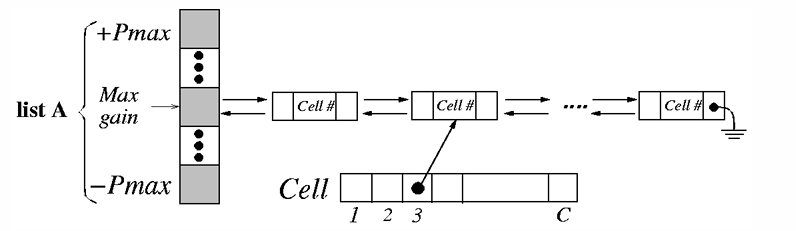
接著集合 A 和 B 個有一個 Size 為 $(2 \cdot P_\text{max} + 1)$ 的 Bucket List，每個 Entry 代表一個 Gain 的值，每個 Entry 裡面存放 Gain 值相同的 Cell 的編號，用 Doubly Linked List 儲存起來

$P_\text{max}$ 是所有 Cell 中 Pin 數量最多那個值

除此之外，還會有個 Cell Array，每個 Cell 有一個指標指向它在 Bucket List 中的位置，這樣可以在 $O(1)$ 的時間內找到目標 Cell

最後，Bucket 裡面還有一個 Max Gain 變數，用來記錄這個集合中最大的 Gain 值，就可以藉由這個變數去找目標 Entry 的第一個 Cell，也就是 Gain 最大的 Cell

Bucket List

Net Distribution and Critical Nets

  • Distribution of Net i 的定義

    $(A(i), B(i)) = (2, 3)$ 代表 Net $i$ 有 2 個 Pin 在 A，3 個 Pin 在 B

    計算所有 Net 的 Distribution 的時間複雜度是 $O(P)$

  • Critical Nets

    如果移動任何一個 Cell 會改變這個 Net 的 Cutstate，這個 Net 就稱為 Critical Net。

    可以想像只有 Cut->Uncut 或 Uncut->Cut 兩種情況，因此只會發生在 移動前後所有 Pin 都在同一邊 的情況下，也就是

    $$
    (A(i), B(i)) = (0, n(i)) \text{ or } (n(i), 0)
    $$

    只有 Critical Nets 才會影響 Gain 的計算

Critical Nets

Computing Cell Gains

一開始要對每個 Cell Iterate 一次所有連到它的 Net ，藉此計算它的 Gain，時間複雜度為 $O(P)$

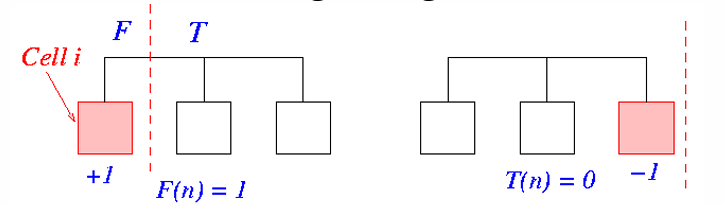
Computing Cell Gains Example

可以看到對於某 Net $n$，在 $F(n) = 1$ 時，移動這個 Cell $i$ 會讓 Net $n$ 從 Cut 變成 Uncut，因此這個 Net 對於這個 Cell 貢獻的 Gain 就是 1

另一種情況是當 $T(n) = 0$ 時，移動這個 Cell $i$ 會讓 Net $n$ 從 Uncut 變成 Cut，因此這個 Net 對於這個 Cell 貢獻的 Gain 就是 -1

Algorithm for Updating Cell Gains

Algorithm for Updating Cell Gains

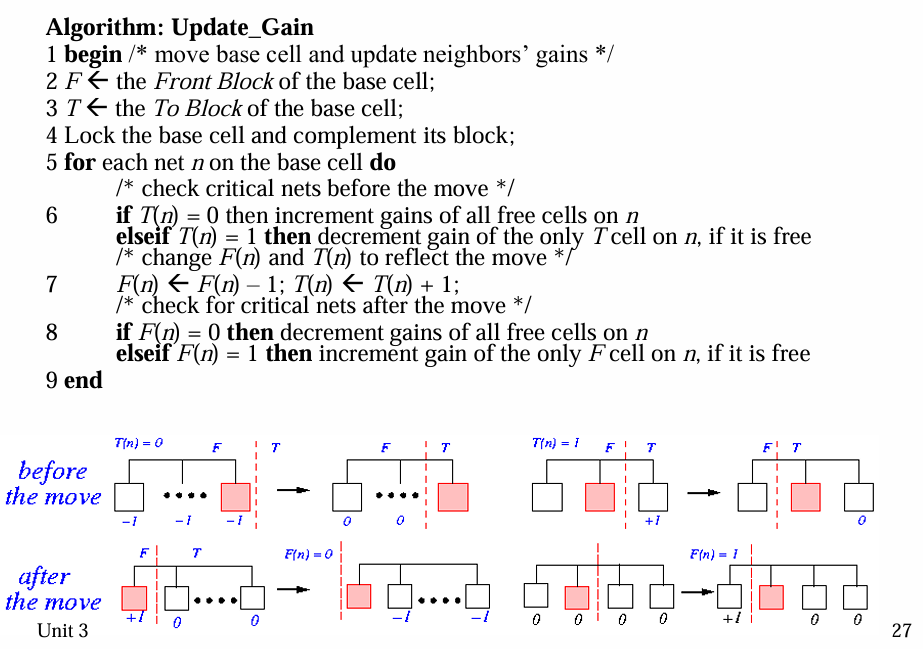
只要想成 目標是 Cut Size 越小越好，所以要找 Gain 最大的 Cell，我們越傾向於移過去某 Cell 後 Net 會變 Uncut 的情況，因此該 Net 對於該 Cell 的 Gain 就是 1，反之越不希望 Net 變 Cut，該 Net 對於該 Cell 的 Gain 就是 -1

每次 Update 的時間複雜度是 $O(P)$

Simulated Annealing (SA) Algorithm

感覺很像機器學習，目的是找到 Global Optimal Solution，但常常會卡在 Local Optimal Solution

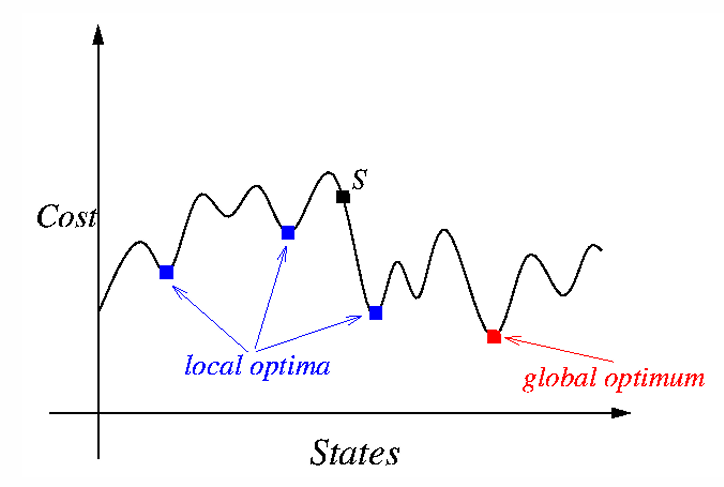
Simulated Annealing

Basics

概念是讓 up-hill move 出現的機率不為 0，其機率會由 up-hill 的量和溫度 T 來決定

$$
\text{Prob}(S \rightarrow S^\prime) = \begin{cases}
1 & \text{if } \Delta C \leq 0 \
e^{-\Delta C / T} & \text{if } \Delta C > 0
\end{cases}
$$

  • 其中
    • $\Delta C$ 是 Cost 的變化量，$\text{Cost}(S^\prime) - \text{Cost}(S)$
    • $T$ 是溫度，隨著時間遞減，讓 up-hill move 的機率越來越小，因此 $T_i = r^i \cdot T_0$，$r$ 是一個介於 0 和 1 之間的常數

Generic SA Algorithm

Generic SA Algorithm

早期受限於記憶體大小，不會把曾經算過的最佳解存起來，這裡就是偏早期的作法

可以看到 SA 構成的四大要素為

  • Solution Space: 所有可能的解
  • Neighborhood Structure: 定義了如何從一個解移動到另一個解
  • Cost Function: 用來評估一個解的好壞
  • Annealing Schedule: 決定了溫度如何隨時間變化

Partitioning by SA

在 Partitioning 的問題中

  • Solution Space: 所有可能的 Partition
  • Neighborhood Structure: 一次只搬一個 Cell 到另一邊
  • Cost Function: Cutset 的 Size + Balance 的 Cost
  • Annealing Schedule: 溫度隨時間遞減

其中 Cost Function 的定義為

$$
f = C + \lambda B
$$

  • $C$: Cutset 的 Size
  • $B$: 評估現在 Balance 的程度，又定義成 $B = (|S1| - |S2|)^2$
  • $\lambda$: 一個常數，用來決定 Balance 的重要程度

Annealing Schedule 的定義為

$$
T_i = r^i \cdot T_0
$$

  • $r$ 通常定成 0.9
  • 每當 每個 Cell 平均成功移動 10 次 或 嘗試移動次數超過 100 * 總 Cells 數量 的情況發生，就把溫度調成 $r$ 倍
  • 如果 連續 3 種溫度都沒有移動成功 就結束，像是機器學習的 Early Stopping

Multi-Level Partitioning

可以分成三個步驟

  1. Coarsening
    把許多小 Cell 合併成大 Cell，也就是把 Graph 變成更小的 Graph，這樣可以減少計算量。通常會做很多次 Coarsening

  2. Initial Partitioning
    在 Coarsest 的 Graph 上做 Partitioning (KL、FM、SA)

  3. Uncoarsening
    把 Initial Partitioning 的結果做 Uncoarsening，把一些原本併在一起的 Cells 拆開，放大整個 Graph，可以想像原本在 A 集合的 Cells 做 Uncoarsening 後還是在 A 集合。

    做了 Uncoarseing 後，相當於得到一個更好的 Initial Solution，再做一次 Partitioning，收斂的速度會很快，結果也會比較好

    也會做很多次 Uncoarsening，變回最原始的 Graph

Multi-Level Partitioning

Coarsening Algorithm

  • Edge coarsening
    兩兩合併
  • Hyperedge coarsening
    會選一組 hyperedges set，把每個 hyperedge 連接到的 Vertices 都合併成一個 Cluster
  • Modified hyperedge coarsening
    先做 Hyperedge coarsening 後，再把剩下落單的 Vertex 合併成一個 Cluster

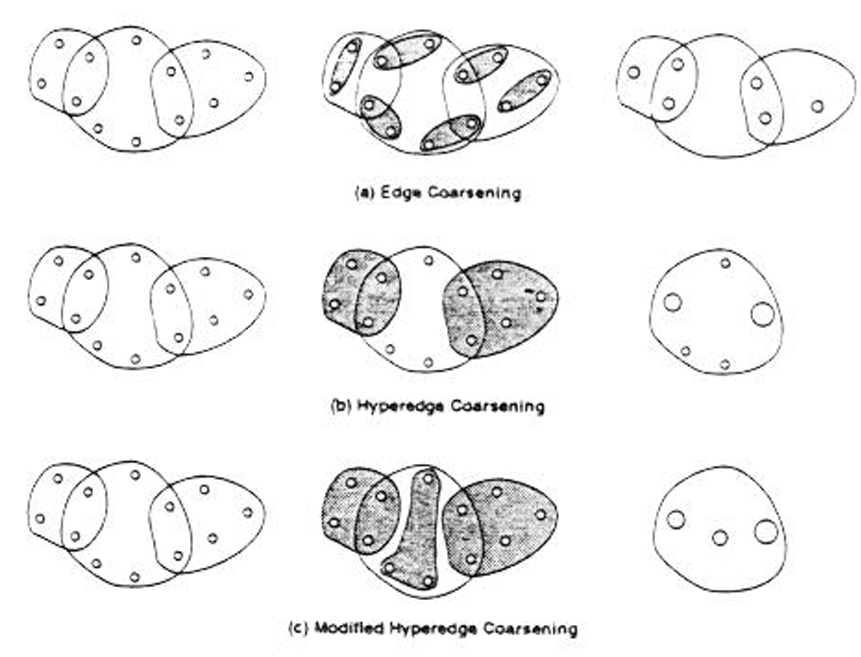
Coarsening Algorithm

Assignment

HW1

Setup

  • Synopsys Design Constraints (.sdc) file
    是一種用來描述 Timing Constraints 的檔案，可以用來告訴 Synthesis Tool 或 Place & Route Tool 一些 Timing 的限制，例如：Clock Period、Setup Time、Hold Time、Clock Latency 等等

  • Library Exchange Format (.lef) file

    用在 PnR，描述 Standard Cell、Macro Cell 的 Physical Layout Information，包含 Standard Cell 的物理邊界、Macro 的位置與大小、金屬層的 Routing 規則、VDD/VSS 的連線資訊、Via 的位置等等

    Import LEF 讓工具知道 Standard Cell 和 Macro 的物理尺寸，以及哪些 Metal Layer 可以用來做 Routing

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    UNITS
    DATABASE MICRONS 1000 ; // 1 LEF unit = 1 nm
    END UNITS

    // Metal Layer
    LAYER M1
      TYPE ROUTING ;
      DIRECTION HORIZONTAL ;
      PITCH 0.14 ;
      WIDTH 0.07 ;
    END M1

    // Standard Cell
    MACRO INVX1
      CLASS CORE ;
      SIZE 0.5 BY 1.2 ;
      PIN A
        DIRECTION INPUT ;
        USE SIGNAL ;
        PORT
          LAYER M1 ;
          RECT (0.1 0.2) (0.2 0.3) ;
        END
      END A
    END INVX1

  • MMMC (Multi-Mode Multi-Constraint) file
    為了確保晶片能夠在所有情境下正常運行，像是：高電壓、低電壓、高溫、低溫甚至 Process Variation 等等，這些變因會影響 Timing 和 Power，因此要可以用 MMMC 來描述這些情境，考慮所有的組合，讓晶片在所有情境下都能正常運作

  • None-Negative Slack
    Slack 是指某個 Timing Path 的 Delay 跟 Constraint 之間的差值，None-Negative Slack 代表這個 Path 是符合 Timing Constraint 的

  • innovus setDesignMode -process 7 -node N7
    設定 Design Mode 為 7nm 的製程，並且設定製成技術為 N7

  • setDesignMode -bottomRoutingLayer 2
    設定最底層的 Routing Layer 為 Metal 2，讓 PnR 工具知道 Global Routing 的從這一層開始

Pre-power planning and Floorplan

確保所有 Standard Cells、Macro、Clock Tree 與電源網絡 Power Network 都能正確擺放，為之後 PnR 做準備。Pre-Power Planning 設定 Global Net，確保所有元件都能正確連接到 VDD 和 VSS

  • Core Size by Aspect Ratio (H/W = 1.0)
    指定 Floorplan 的 Core Size，這裡是正方形

  • Core Utilization
    指定 Core 的使用率，0.4 代表 Standard Cell 的面積佔整個 Core 的 40%，剩下的 60% 留給 Routing，太高會影響 Routing 或 Timing

  • Core to Die Boundary
    Core 與 Die 的邊界之間的間距，通常會留一些空間給 I/O Pads、Power Pads、Bumps

  • Tool Command Language (.tcl) file
    類似於 Shell Script，可以用來執行一連串的指令，例如：Synthesis、Place & Route、Simulation 等等

  • Well Tap Cell
    避免 Latch-up，連接 P-Well 到 GND (NMOS)，N-Well 到 VDD (PMOS)

    1
    addWellTap -cell TAPCELL_ASAP7_75t_L -cellInterval 12.960 -inRowOffset 1.296
    • 在 Core 區域內，每隔 12.960 µm 插入 Well Tap Cell，並偏移 1.296 µm 來對齊。

Power Planning

  • Power Ring
    在 Core 周圍建立一個封閉的電源環，讓所有元件都能夠穩定的接上 VDD 和 VSS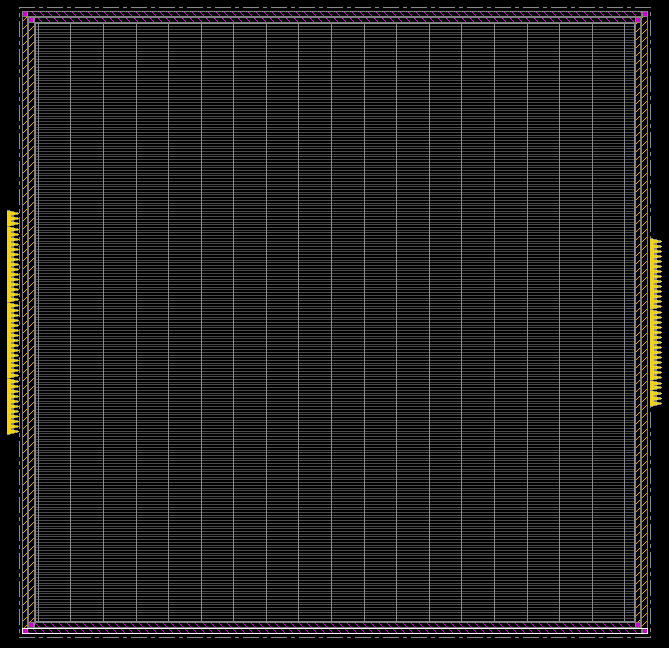

    Power Ring

  • Power Stripes
    在 Core 內部建立一個電源線，連到 Power Ring，形成完整的 Power Network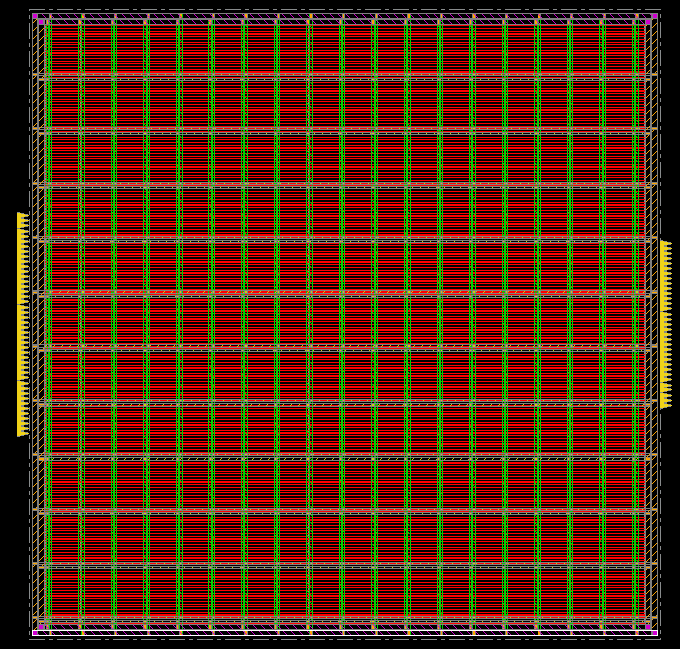

    Power Stripes

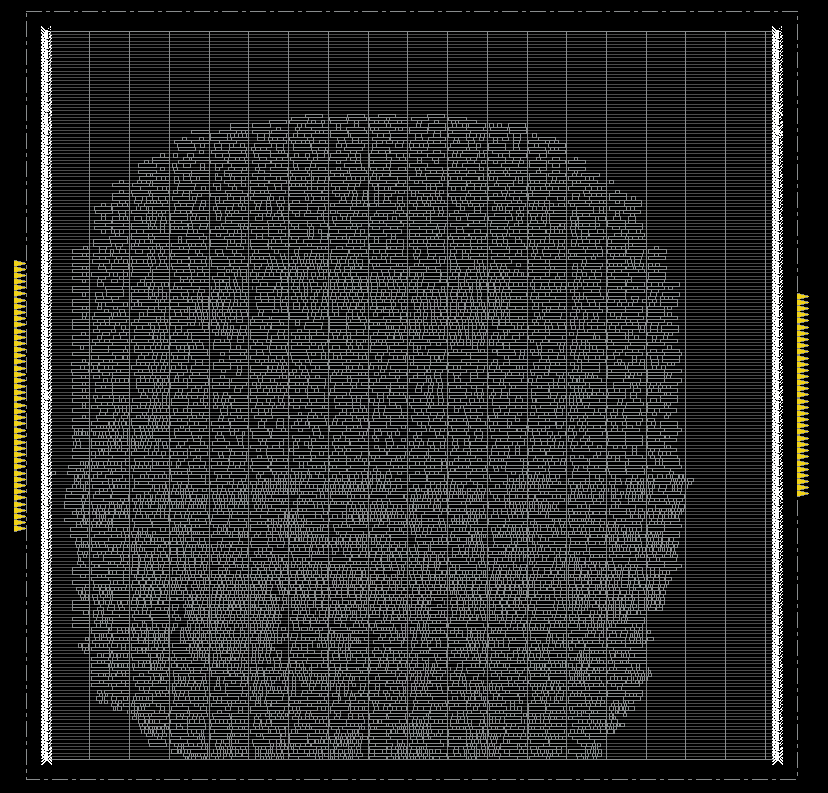
Placement (place_opt_design)

  • Placement
    把所有 Standard Cells、Macro Cells 放到 Floorplan 的 Core 內

  • Placement Optimization
    透過 Placement Optimization 來最佳化 Placement，達到 Power Optimization 或 Timing Optimization

Placement

Clock Tree Synthesis

CLK 控制晶片裡所有 Flip-Flop 的 Timing，要確保所有 Flip-Flop 都能在同一個 Clock Cycle 內正確的被觸發

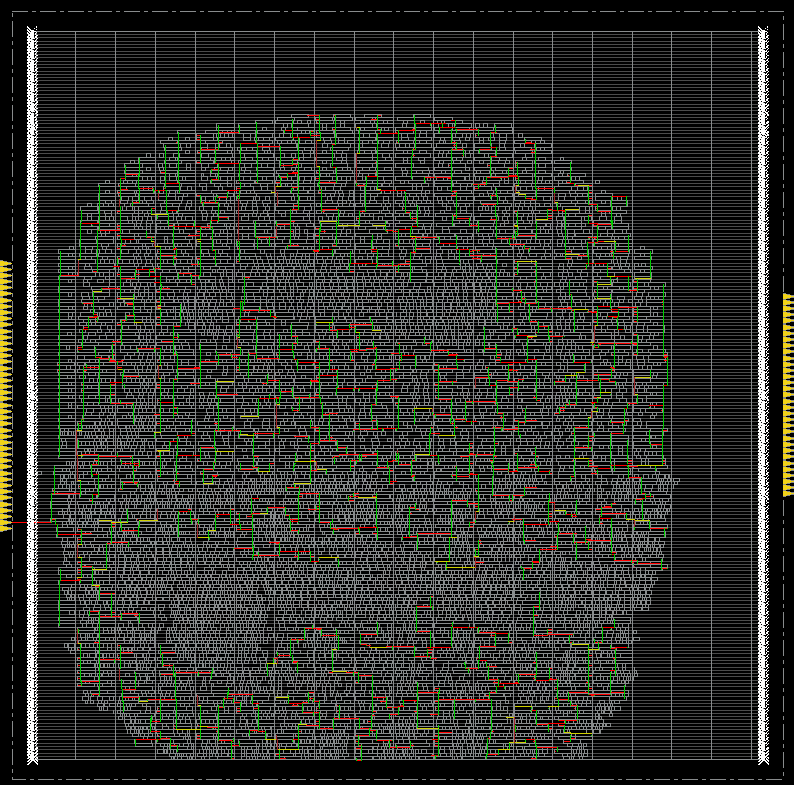
Clock Tree Synthesis

圖中的紅色、綠色、黃色線就是 CLK 訊號

Routing

  • routeDesign
    將所有標準單元、Macro 之間的連線轉換為實際金屬導線，並確保符合 Timing 和 DRC 規則，自動插入 Via 連接不同金屬層

Routing

VLSI
#vlsi #physical design #automation
VLSI PDA - Partitioning
https://933yee.github.io/notes/2025/02/25/vlsi-physical-design-automation-2/
Author
Kevin Lee
Posted on
February 25, 2025
Licensed under