Machine Learning - Training Difficulties

惡補 ML https://www.youtube.com/watch?v=Ye018rCVvOo&list=PLJV_el3uVTsMhtt7_Y6sgTHGHp1Vb2P2J

類神經網路訓練不起來

卡在 Critical Point

• Local Minimum
• Saddle Point

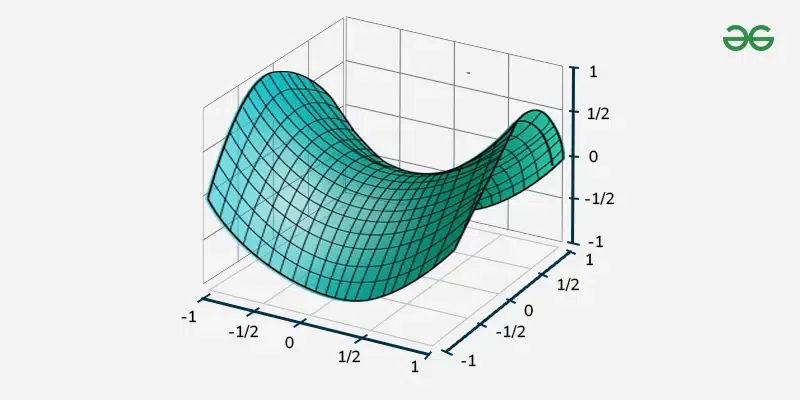
泰勒展開式

對於 $L(\theta)$，在 $\theta = \theta^\prime$ 可以被近似為：

$$
L(\theta) \approx L(\theta^\prime) + (\theta - \theta^\prime)^T \cdot g + \frac{1}{2}(\theta - \theta^\prime)^T \cdot H \cdot (\theta - \theta^\prime)
$$

• $g$ 為 Gradient Vector，$g = \nabla L(\theta^\prime)$
• $H$ 為 Hessian Matrix，$H = \nabla^2 L(\theta^\prime)$

當走到 Critical Point 時，Gradient 會等於 0，所以可以得到：

$$
L(\theta) \approx L(\theta^\prime) + \frac{1}{2}(\theta - \theta^\prime)^T \cdot H \cdot (\theta - \theta^\prime)
$$

因此可以利用 Hessian Matrix 來判斷是 Local Minimum 、 Local Maximum 還是 Saddle Point

• 當 $\frac{1}{2}(\theta - \theta^\prime)^T \cdot H \cdot (\theta - \theta^\prime) > 0$ 時，可以知道任何在 $\theta^\prime$ 附近的 $\theta$，$L(\theta) > L(\theta^\prime)$ ，所以 $L(\theta^\prime)$ 是 Local Minimum
• 當 $\frac{1}{2}(\theta - \theta^\prime)^T \cdot H \cdot (\theta - \theta^\prime) < 0$ 時，可以知道任何在 $\theta^\prime$ 附近的 $\theta$，$L(\theta) < L(\theta^\prime)$ ，所以 $L(\theta^\prime)$ 是 Local Maximum
• 當 $\frac{1}{2}(\theta - \theta^\prime)^T \cdot H \cdot (\theta - \theta^\prime)$ 有時候大於 0 有時候小於 0 時， $\theta^\prime$ 是 Saddle Point

基於線性代數的知識，可以知道 Hessian Matrix 是 Symmetric Matrix，所以可以透過 Eigenvalue 來判斷是 Local Minimum 、 Local Maximum 還是 Saddle Point

• 當 Hessian Matrix 的 Eigenvalue 全部大於 0 時，是 Local Minimum
• 當 Hessian Matrix 的 Eigenvalue 全部小於 0 時，是 Local Maximum
• 當 Hessian Matrix 的 Eigenvalue 有正有負時，是 Saddle Point

如果是 Saddle Point，可以透過 Hessian Matrix 來判斷出 Loss 更小的方向，然後往那個方向走：

$$
L(\theta) \approx L(\theta^\prime) + \frac{1}{2}(\theta - \theta^\prime)^T \cdot H \cdot (\theta - \theta^\prime)
$$

假設 $u$ 是 Hessian Matrix 的 Eigen vector，$\lambda$ 是 Eigen value，可以得到：

$$
u^T \cdot H \cdot u = u^T \cdot (\lambda \cdot u) = \lambda \lVert u \rVert^2
$$

當 $(\theta - \theta^\prime) = u$ 且 $\lambda < 0$ 時：

$$
\frac{1}{2}(\theta - \theta^\prime)^T \cdot H \cdot (\theta - \theta^\prime) = \frac{1}{2}u^T \cdot H \cdot u = \frac{1}{2}\lambda \lVert u \rVert^2 < 0
$$

可以知道 $L(\theta) < L(\theta^\prime)$。因此如果讓 $\theta^\prime$ 往 $u$ 的方向走，$\theta^\prime + u = \theta$，可以得到更小 Loss 的 $\theta$。

這只是一種解法，在實作上計算量很大，沒有人會這樣做。

此外，實際上 Local minimum 並不常見，Loss 下不去常常是卡在 Saddle Point，但是用一般的 Gradient Descent 通常不會卡在 Critical Point。

為什麼要用 Batch

• Batch size = N(Full Batch)

  • 一次拿所有資料去算 Gradient
  • 每一次的 Gradient 都很穩定
  • 理論上花的時間比較多，但考慮到平行運算，若以 epoch 為單位，實際上可能更快

• Batch size = 1

  • 一次只拿一筆資料去算 Gradient
  • 每一次的 Gradient 都很不穩定，可能會跳來跳去

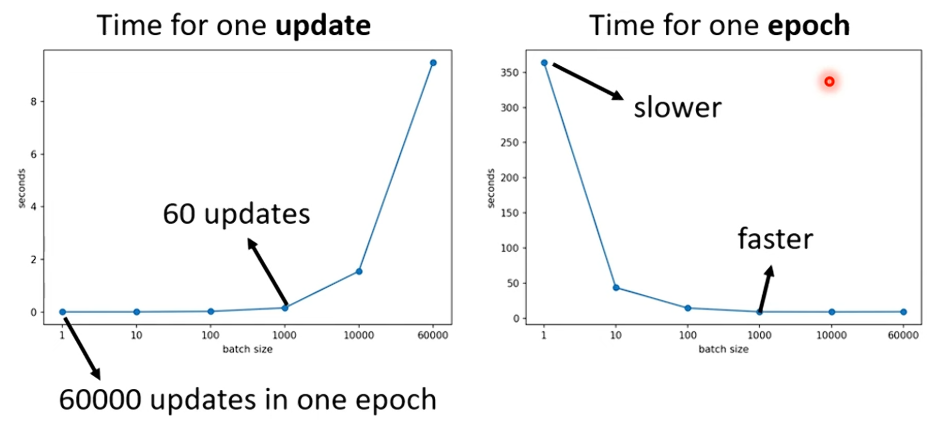
既然時間差不多，乍看之下 Batch Size 大一點比較好，但實際上小的 Batch Size 可能會有更好的訓練效果

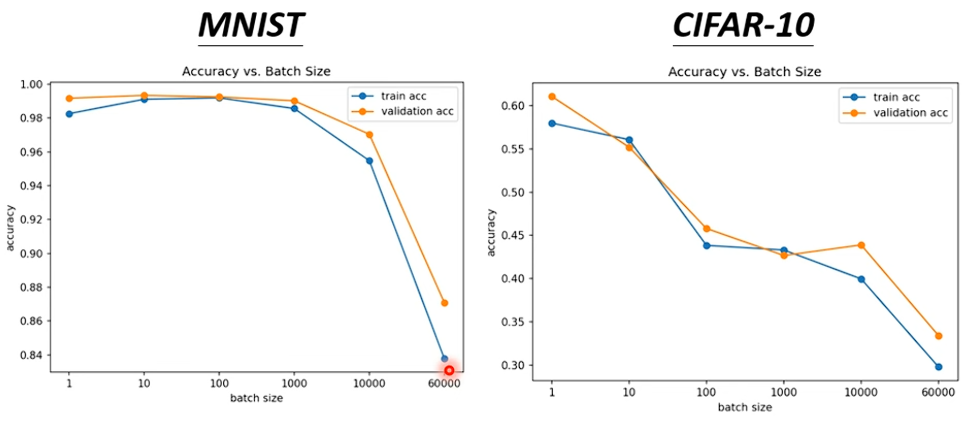
上圖可以看到小的 Batch Size Optimization 的效果會比較好

	Batch Size 小	Batch Size 大
每次 update (沒有平行運算)	快	慢
每次 update (有平行運算)	一樣	一樣 (在不是超大的情況下)
每個 epoch	慢	快
Gradient 的穩定性	差	穩定
Optimization 的效果	好	差

Momentum

• 一般的 Gradient Descent

  • $\theta_{t+1} = \theta_t - \eta \cdot \nabla L(\theta_t)$

• Momentum

  $$
  \begin{aligned}
  \texttt{Start at} \quad \theta^0 \newline
  \texttt{Movement} \quad m^0 &= 0 \newline
  \texttt{Compute gradient} \quad g^0 \newline
  \texttt{Movement} \quad m^1 &= \lambda \cdot m^0 - \eta \cdot g^0 \newline
  \texttt{Move to} \quad \theta^1 &= \theta^0 + m^1 \newline
  \texttt{Compute gradient} \quad g^1 \newline
  \texttt{Movement} \quad m^2 &= \lambda \cdot m^1 - \eta \cdot g^1 \newline
  \texttt{Move to} \quad \theta^2 &= \theta^1 + m^2 \newline
  \end{aligned}
  $$

  $m^i$ 就像是所有過去 Weighted Gradient 的總和，$g^0, g^1, \cdots g^{i-1}$

  $$
  \begin{aligned}
  m^0 &= 0 \newline
  m^1 &= \lambda \cdot m^0 - \eta \cdot g^0 \newline
  &= -\eta \cdot g^0 \newline
  m^2 &= \lambda \cdot m^1 - \eta \cdot g^1 \newline
  &= \lambda \cdot (-\eta \cdot g^0) - \eta \cdot g^1
  \end{aligned}
  $$

  

Learning Rate

一般情況下的 Learning Rate 造成的問題

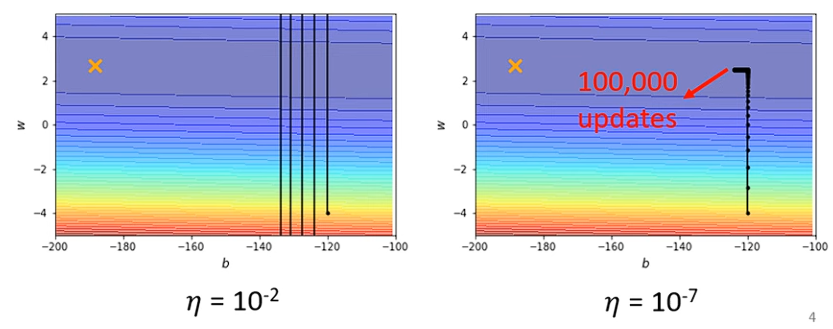
• 當 Learning Rate 設定太大時，可能會造成 Oscillation 的問題，Loss 會一直在上下跳動，無法收斂
• 當 Learning Rate 設定太小時，可能會造成 Convergence 的問題，Loss 會一直往下收斂，但是收斂的速度很慢。就像上圖一樣，當 Gradient 很大時，沒什麼問題，但是當 Gradient 很小時，就會卡住

上述例子中，每個參數的 Learning Rate 都是一樣的，但是實際上每個參數的 Gradient 都不一樣，應該要為每個參數的 Learning Rate 客製化。

AdaGrad (Adaptive Gradient)

用 Root Mean Square 來調整 Learning Rate

$$
\begin{aligned}
\theta^1_i \leftarrow \theta^0_i - \frac{\eta}{\sigma^0_i} \cdot g^0_i &\quad \sigma^0_i = \sqrt{(g^0_i)^2} = \lvert g^0_i \rvert \newline
\theta^2_i \leftarrow \theta^1_i - \frac{\eta}{\sigma^1_i} \cdot g^1_i &\quad \sigma^1_i = \sqrt{\frac{1}{2} \cdot [(g^0_i)^2 + (g^1_i)^2]} \newline
\theta^3_i \leftarrow \theta^2_i - \frac{\eta}{\sigma^2_i} \cdot g^2_i &\quad \sigma^2_i = \sqrt{\frac{1}{3} \cdot [(g^0_i)^2 + (g^1_i)^2 + (g^2_i)^2]} \newline
\vdots \newline
\theta^{t+1}_i \leftarrow \theta^t_i - \frac{\eta}{\sigma^t_i} \cdot g^t_i &\quad \sigma^t_i = \sqrt{\frac{1}{t} \cdot \sum^t_k (g^k_i)^2}
\end{aligned}
$$

從公式可以觀察到，當坡度小的時候，Gradient 會比較小，算出來的 $\sigma$ 也會比較小，所以 Learning Rate 會比較大，反之亦然。

然而，當 t 很大時，當前的 Gradient 可能會被過去累積的 Gradient 稀釋掉，導致收斂速度變慢，不能實時考慮梯度的變化情況。

RMSprop

RMSprop 增加了 Decay Rate $\alpha$，可以控制 當前的 Gradient 和 過去累積的 Gradient 的重要程度

$$
\begin{aligned}
\theta^1_i \leftarrow \theta^0_i - \frac{\eta}{\sigma^0_i} \cdot g^0_i &\quad \sigma^0_i = \sqrt{(g^0_i)^2} = \lvert g^0_i \rvert \newline
\theta^2_i \leftarrow \theta^1_i - \frac{\eta}{\sigma^1_i} \cdot g^1_i &\quad \sigma^1_i = \sqrt{\alpha \cdot (\sigma^0_i)^2 + (1 - \alpha) \cdot (g^1_i)^2} \newline
\theta^3_i \leftarrow \theta^2_i - \frac{\eta}{\sigma^2_i} \cdot g^2_i &\quad \sigma^2_i = \sqrt{\alpha \cdot (\sigma^1_i)^2 + (1 - \alpha) \cdot (g^2_i)^2} \newline
\vdots \newline
\theta^{t+1}_i \leftarrow \theta^t_i - \frac{\eta}{\sigma^t_i} \cdot g^t_i &\quad \sigma^t_i = \sqrt{\alpha \cdot (\sigma^{t-1}_i)^2 + (1 - \alpha) \cdot (g^t_i)^2}
\end{aligned}
$$

• $\alpha$ 為 Decay Rate，通常設為 0.9

最常用的 Optimizer 是 Adam，他就是 RMSprop 和 Momentum 的結合

Learning Rate Scheduling

• Learning Rate Decay

  隨著參數的更新，Learning Rate 逐漸變小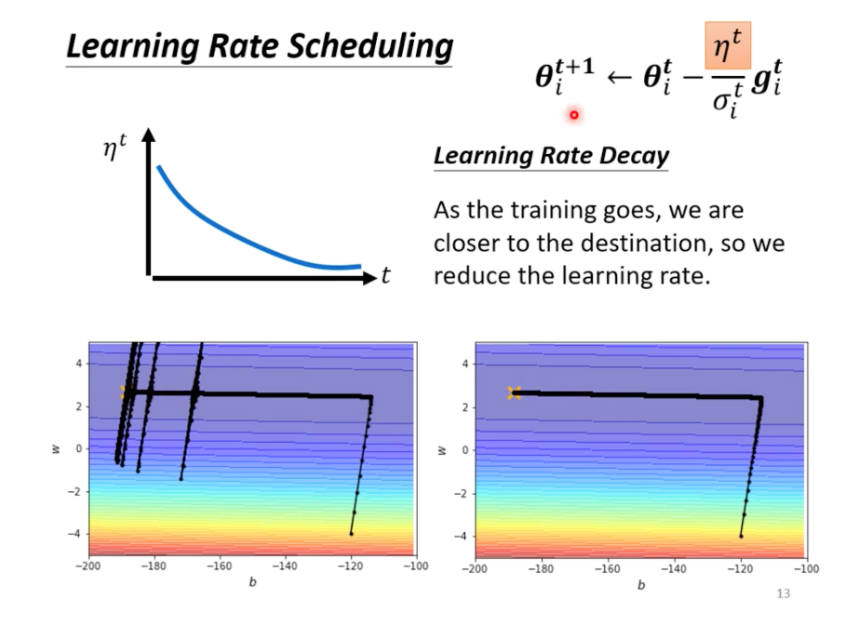

  

  左邊是 AdaGrad，當縱軸的 Gradient 一直都是很小的值時，會導致 $\sigma$ 變得很小，造成 Learning Rate 放的很大，因此會飛出去。右邊是加上 Learning Rate Decay。

• Warm Up

  在一開始的時候，Learning Rate 會比較小，然後逐漸變大，最後再變小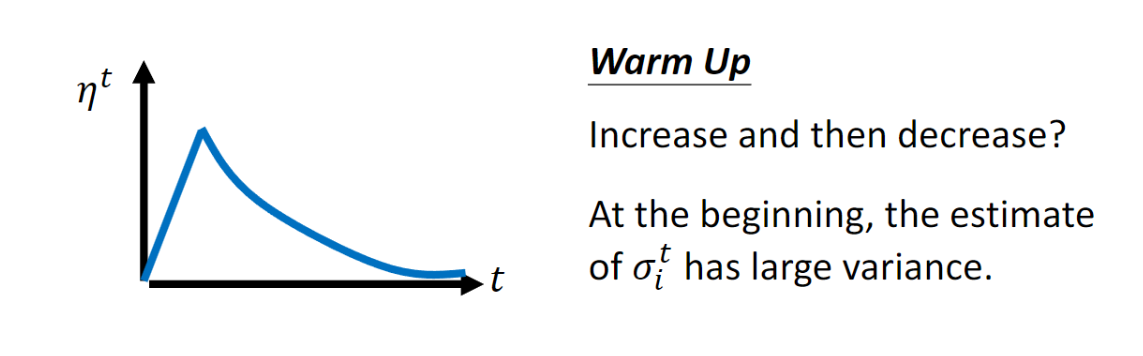

  

Loss Function

Loss Function 也會影響到 Optimization 的效果，這邊以分類問題為例。

Classification

在 Classification 的問題中，通常會用 one-hot encoding 來表示 label，例如：

$$
\begin{aligned}
\hat{y} &= [1, 0, 0] \newline
\hat{y} &= [0, 1, 0] \newline
\hat{y} &= [0, 0, 1] \newline
\end{aligned}
$$

最後在 Output 的時候，通常會把輸出 y 通過 Softmax 函數，再讓他和 one-hot encoding 的 label 做比較，計算出 Loss

$$
\begin{aligned}
\text{Softmax}(z)_i &= \frac{e^{z_i}}{\sum^n_j e^{z_j}} \newline
\hat{y} \leftrightarrow y^\prime &= \text{Softmax}(y) \newline
\end{aligned}
$$

• 這裡的 y 稱為 logit
• Softmax 可以把 Output 變成 Probability，讓 Output 的值在 0 到 1 之間，並且總和為 1
• 當只有兩個 Class 時，Softmax 和 Sigmoid 的作用是一樣的

Loss Function of Classification

可以直接用 MSE，但是 Cross-entropy 通常表現的比較好

• Cross-entropy
  $$L = -\sum_{i=1}^{n} \hat{y_i} \cdot \ln(\hat{y}_i)$$
  • Minimize Cross-entropy 就是最大化 Likelihood

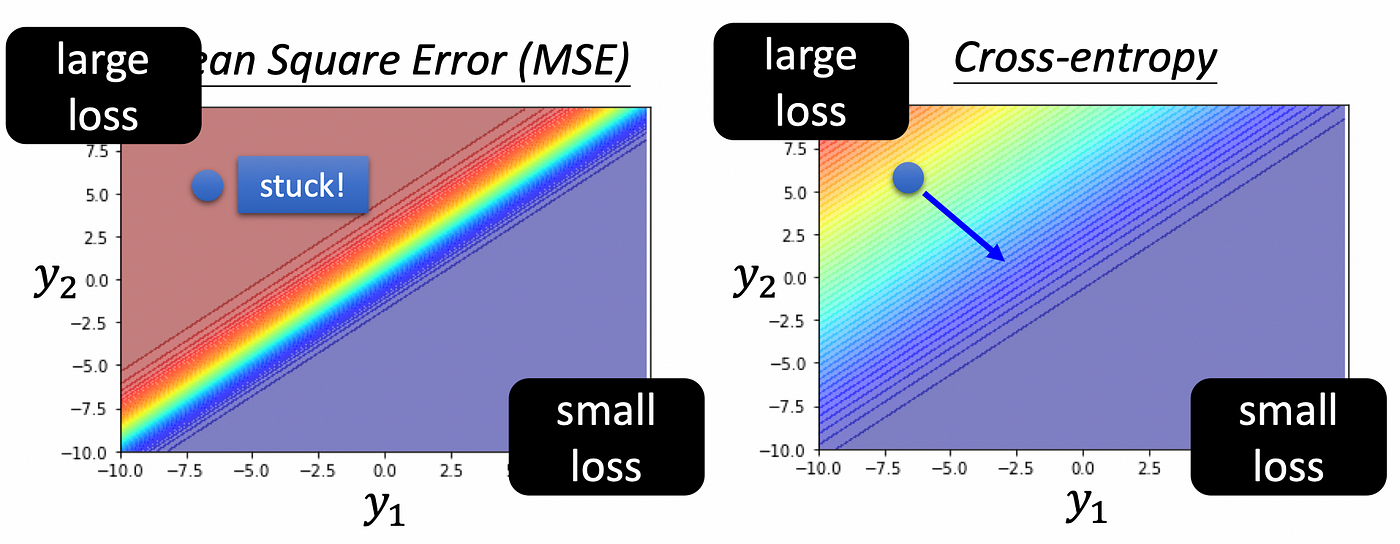
上圖可以看到，在 Classfication 問題用 MSE 可能會 train 不起來

Batch Normalization

有時候在 Error Surface 中，不同維度的輸入值可能差很多，導致 Error Surface 很扭曲，斜率、坡度都不同

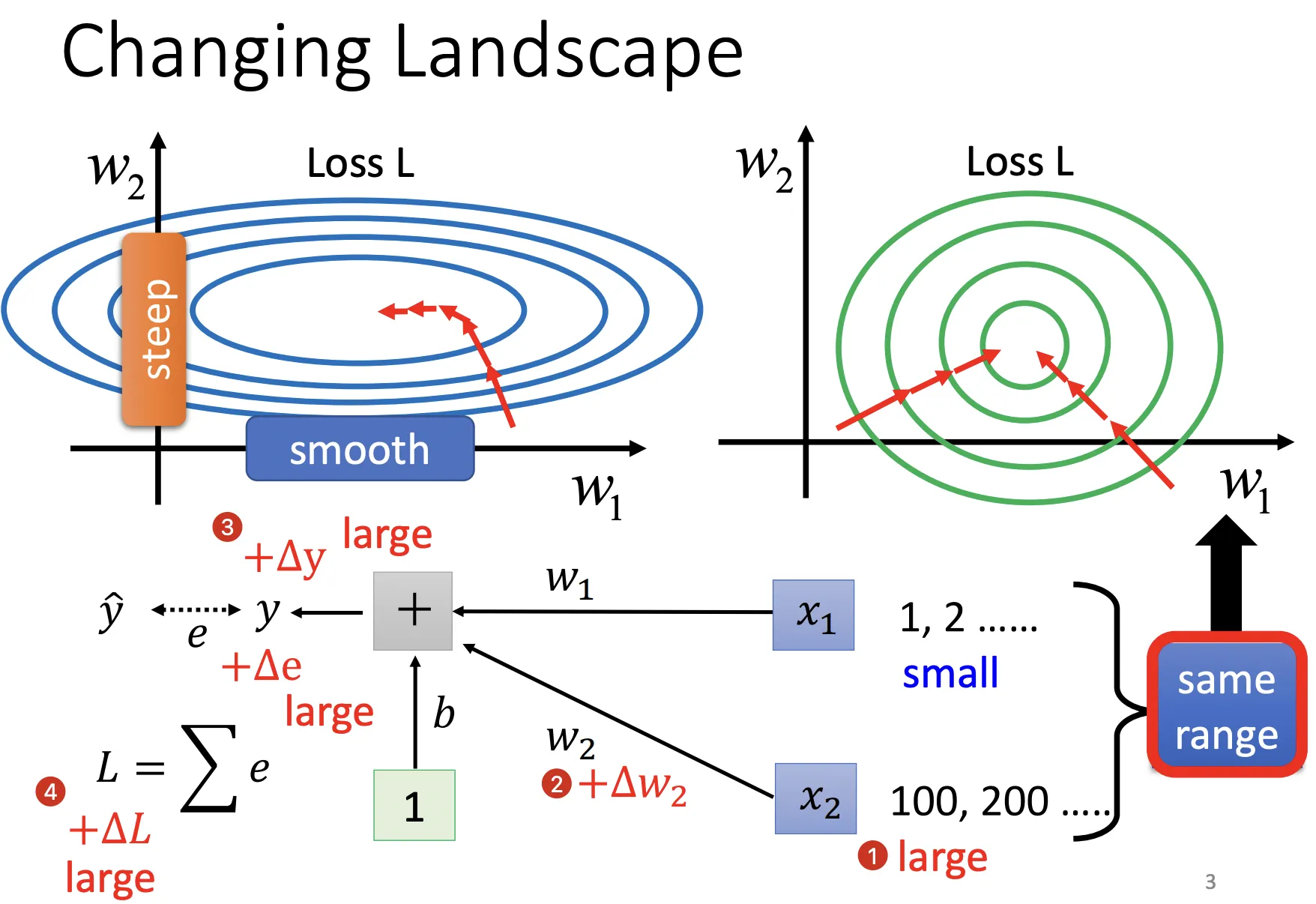
對於一個 Batch 的資料，對每一個 Feature 做 Feature Normalization，讓他的 Mean 為 0，Variance 為 1，稱為 Batch Normalization

$$
\begin{aligned}
\mu &= \frac{1}{m} \sum_{i=1}^{m} x_i \newline
\sigma^2 &= \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu)^2 \newline
\hat{x}_i &= \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}} \newline
\end{aligned}
$$

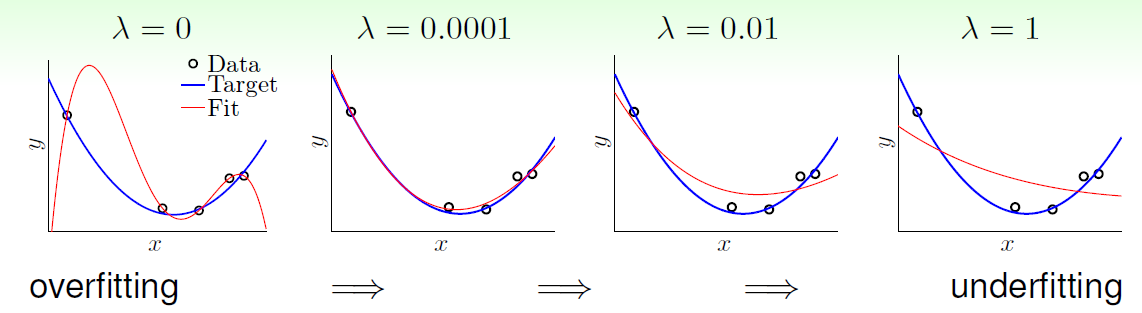
Regularization

最常使用 L1 和 L2 Regularization，在 Loss Function 中加上 Regularization Term，讓 Model 不要太複雜

公式來源可以參考 Lagrange Multiplier。

L1 Regularization

$$
Loss_Fn = original_Loss_Fn + \lambda \cdot \sum_{i=1}^{n} \lvert w_i \rvert
$$

L2 Regularization

$$
Loss_Fn = original_Loss_Fn + \lambda \cdot \sum_{i=1}^{n} w_i^2
$$

參考資料

• L1 , L2 Regularization 到底正則化了什麼 ?