VLSI DFM - Maze Routing

參考清大麥偉基老師課程講義

Lithography

• Lithography: 光刻
  框出電路圖案，然後進行蝕刻
• Diffraction: 繞射
  會造成 Lithography 不準確，可以從目標圖案反推出 Mask 的設計，稱為 Computational Lithography

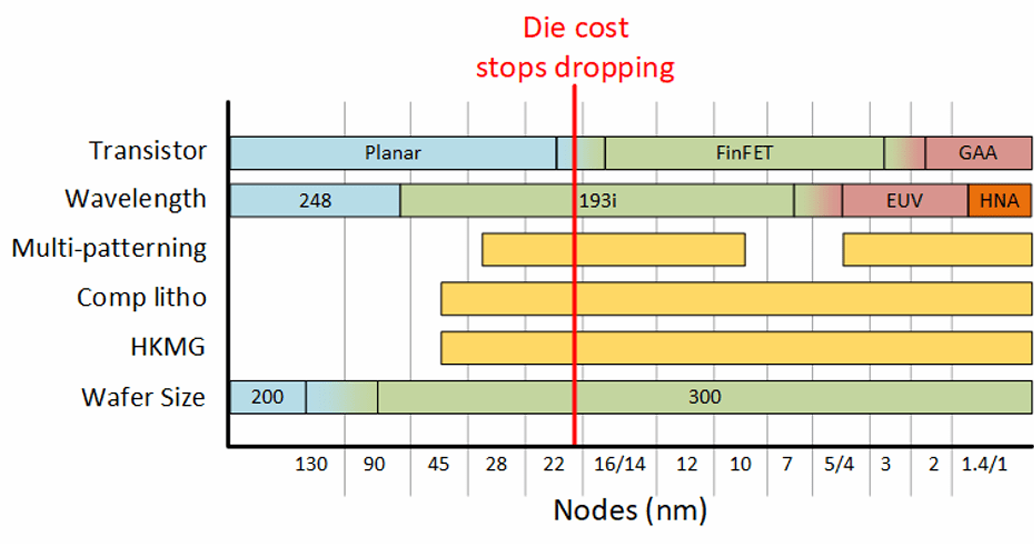
• 193i 的 i 代表 Immersion Lithography
  用液體取代空氣，縮短光的波長，就好像換了一個 Light Source，減少繞射的影響，而且波長 193nm 的技術已經很成熟
• EUV 代表 Extreme Ultraviolet Lithography
  波長更短，繞射更少，但是製程更難，因為要用真空，光源也很難做
• Multi-Patterning
  把一個圖案分成多個小圖案，然後分別曝光，最後合併成一個圖案。在 EUV Lithography 之前很常用，現在因為 EUV 很貴，有些先進製程還是用 193i + Multi-Patterning
• 隨著技術進步，單位面積上的 Transistor 數量越來越多，但是製程成本也越來越高，所以不是每個裝置都用最先進的製程

Routing in Advanced Nodes

受限於 Lithography printability、Process Variation 等，即使你用一樣的方法，做出來的也不一定是你要的。所以要考慮 Design for Manufacturability。

Design Rule Handling

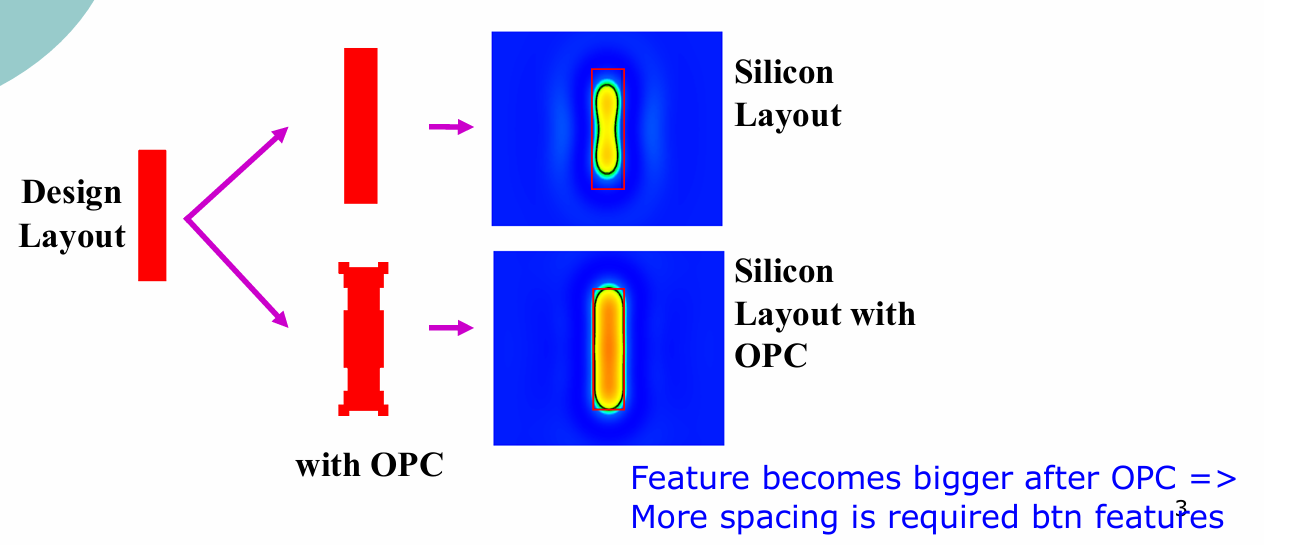
Optical Proximity Correction (OPC) 是一種 Computational Lithography 的技術，修改 mask 來補償繞射和光刻製程中的非理想效應，讓實際製造出的 Pattern 更接近設計的目標。

• OPC 會造成線寬變寬，所以要考慮 Design Rule，ex：兩條線之間要留多少空間

End-to-End Seperation Rule

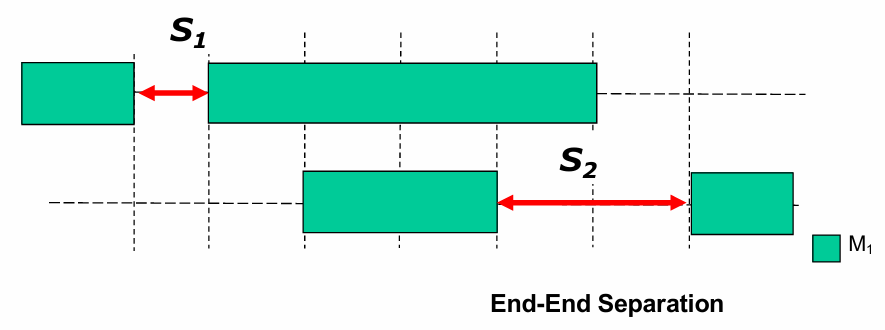
• 如果一條 Wire 的端點的相鄰軌道上有另一條 Wire，那這條 Wire 的末端至少要留 S2 的空間
• 其他情況只需要預留 S1 的空間

Minimum Length Rule

每條線至少要有多長

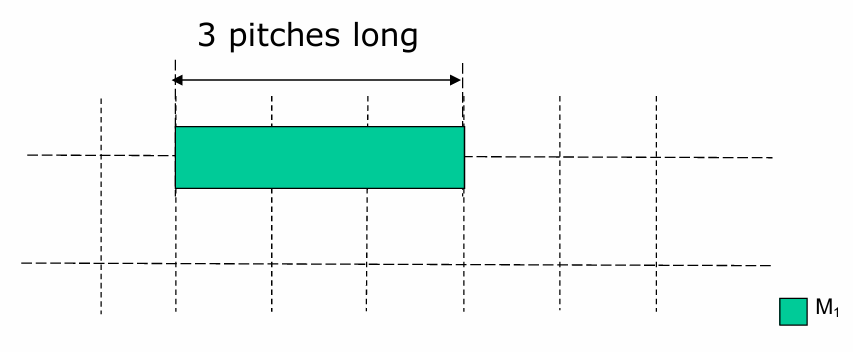
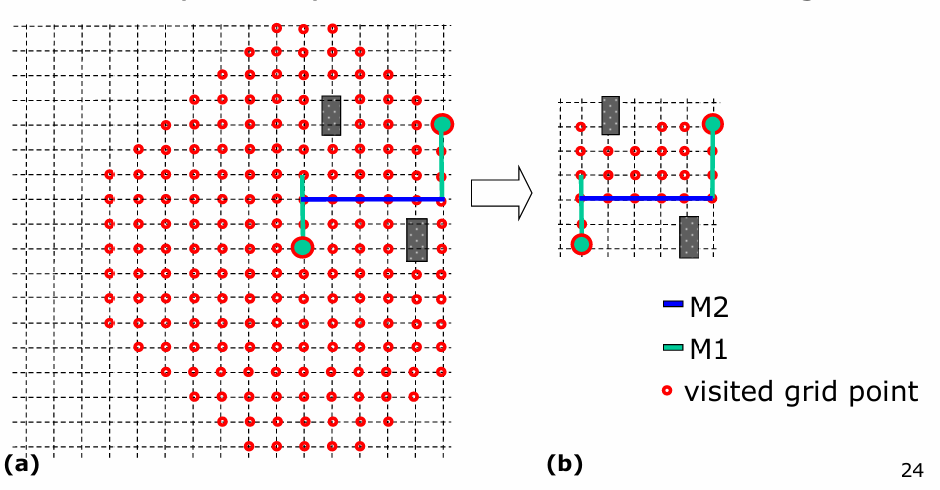
MANA (A Shortest Path MAze Algorithm under Separation and Minimum Length NAnometer Rules)

傳統的 Maze Routing Algorithm 是在 Grid 上找一條最短的路徑，可能用 BFS 或 Dijkstra 等等，但是在 VLSI 設計中，還要考慮一些 Design Rule

考慮到 Design Rule 的 Maze Routing Algorithm

• Post-Processing
  把找到的路徑再做一些調整，像是延伸 Wire，讓他們符合先前提到的 Design Rule，不過這方法沒那麼好，會花很多資源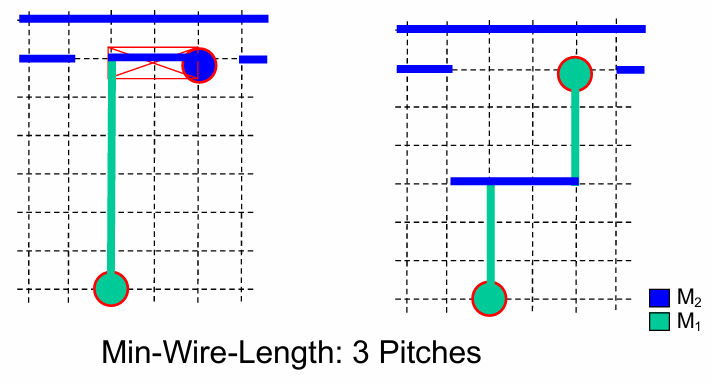

  

• 增強型 Maze Routing Algorithm
  在找路徑的時候就考慮 Design Rule，像是「每條 Wire 至少要有多長」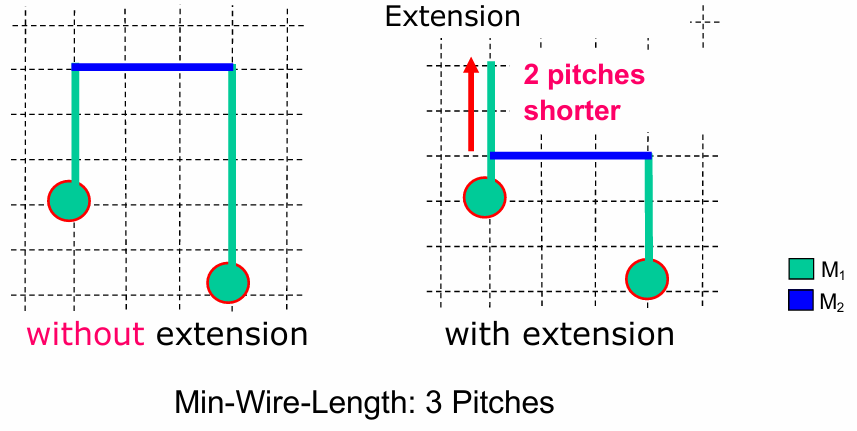
  

  不能直接用個 L 型的 Wire，每一層要馬是水平，要馬是垂直

End-end separation rule handling

檢查每個 grid point，如果這個 grid point 不能滿足 End-end separation，就把它濾掉

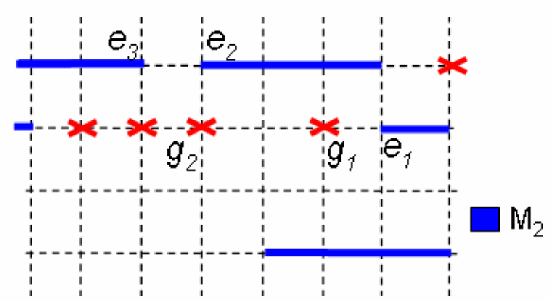
Minimum length rule handling

在做 Maze Routing 的時候，要看這條 wire 有沒有足夠的空間做 extension

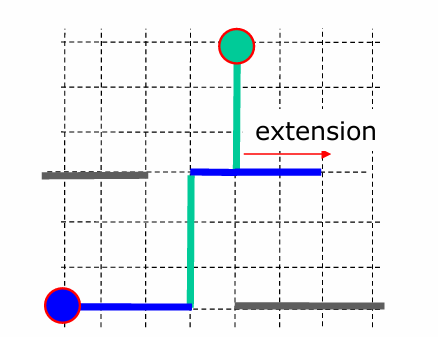
Find a Shortest Path

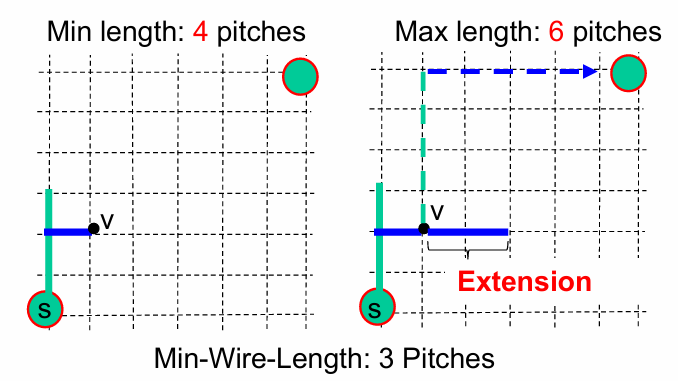
• Min Length: 全部的 wire 長度加起來，不包含最後一段的 extension
• Max Length: 全部的 wire 長度加起來，包含最後一段的 extension

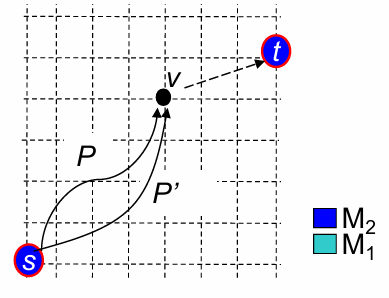
Polynomial time complexity

對不需要的 partial path 做 pruning，可以達到 Polynomial time complexity

像是這邊可以只保留 $P^\prime$，捨棄 $P$

Pruning Strategy

• Stradgy 1

  如果 $\text{minlen}(P) \geq \text{maxlen}(P^\prime)$，就捨棄 $P$

• Stradgy 2

  如果 $\text{maxlen}(P) = \text{maxlen}(P^\prime)$ 且 $\text{minlen}(P) = \text{minlen}(P^\prime)$，兩個一樣好，捨棄其中一個即可

Best Cost-First Expansion

Maze Routing 的演算法本質上是還是 A*-Search，要考慮某個 grid point 和 destination 的 manhattan distance，才能夠有方向性，所以

$$
\text{Cost}(P) = \text{maxlen}(P) + \text{Manhattan dist.}
$$