Deep Learning - NN, CNN & RNN
Neural Networks: Design
Feedforward Neural Networks (FNN) 或 Multilayer Perceptrons (MLP)
可以 Deompose 成:
$$
\begin{aligned}
\hat{y} = f^{(L)}(\ldots f^{(2)}(f^{(1)}(x; \theta^{(1)}); \theta^{(2)}) \ldots; \theta^{(L)})
\end{aligned}
$$
- 會假設 $f$ 是 Non-Linear Function,不然就只是線性模型而已,分那麼多層就沒意義了
- 藉由 Training Set $\mathbf{X}$ 來學習參數 $\Theta = {\theta^{(1)}, \theta^{(2)}, \ldots, \theta^{(L)}}$,來逼近最佳函數 $f^*$
$$
\begin{aligned}
a^{(k)}
&= \text{act}^{(k)}(W^{(k)\top} a^{(k-1)} + b^{(k)}) \newline
\end{aligned}
$$
Neurons
每個 Neuron 的計算方式如下:
$$
f_j^{(k)} = \text{act}^{(k)}(W_{:, j}^{(k)\top} a^{(k-1)}) = \text{act}^{(k)}(z_j^{(k)})
$$
Hidden Layer $f^{(1)}, f^{(2)}, \ldots, f^{(L-1)}$ 的輸出分別是 $a^{(1)}, a^{(2)}, \ldots, a^{(L-1)}$,越深的 Layer 表示越高階的特徵,越抽象
而最後一層 $f^{(L)}$ 的 $\text{act}$ 只是為了把輸出轉換成適合的形式 (e.g. regression, classification)
Training an NN
- 大部分 NNs 是用 maximum likelihood 來訓練的
$$
\begin{aligned}
\text{argmax}{\Theta} \text{log } P(X | \Theta) &= \text{argmin}{\Theta} -\text{log } P(X | \Theta) \newline
&= \text{argmin}{\Theta} \Sigma_i -\text{log } P(x_i, y_i | \Theta) \newline
&= \text{argmin}{\Theta} \Sigma_i [-\text{log } P(y_i | x_i, \Theta) - \text{log } P(x_i | \Theta)] \newline
&= \text{argmin}{\Theta} \Sigma_i -\text{log } P(y_i | x_i, \Theta) \quad \text{(if we ignore } P(x_i | \Theta)) \newline
&= \text{argmin}{\Theta} \Sigma_i C_i (\Theta)
\end{aligned}
$$
$$
\begin{aligned}
C_i(\Theta) &= -\text{log } P(y_i | x_i, \Theta) \newline
&= -\text{log } [(a^{(L)})^{y^{(i)}} (1 - a^{(L)})^{1-y^{(i)}}] \newline
&= -\text{log } [(\sigma(z^{(L)}))^{y^{(i)}} (1 - \sigma(z^{(L)}))^{1-y^{(i)}}] \newline
&= -\log[\sigma(2y^{(i)} - 1) z^{(L)}] \newline
&= \text{softplus}(- (2y^{(i)} - 1) z^{(L)}) \newline
\end{aligned}
$$
Backpropagation
在用 Stochastic Gradient Descent (SGD) 訓練 NN 時,每次更新參數的方式如下:
$$
\Theta^{(t+1)} \leftarrow \Theta^{(t)} - \eta \nabla_{\Theta} \sum_i^M C^{(i)}(\Theta^{(t)})
$$
但是每次都要算 $\nabla_{\Theta} \sum_i^M C^{(i)}(\Theta^{(t)})$ 很麻煩
令 $c^{(n)} = C^{(n)}(\Theta^{(t)})$,則會需要計算所有 $i, j, k, n$ 的偏微分
$$
\frac{\partial c^{(n)}}{\partial W_{i, j}^{(k)}}
$$
但其實計算過程中有很多重複的計算,所以可以用 Backpropagation 的方式節省計算量
根據 Chain Rule,我們有
$$
\frac{\partial c^{(n)}}{\partial W_{i, j}^{(k)}} = \frac{\partial c^{(n)}}{\partial z_j^{(k)}} \frac{\partial z_j^{(k)}}{\partial W_{i, j}^{(k)}}
$$
Forward Pass
目標是計算第二項
$$
\frac{\partial z_j^{(k)}}{\partial W_{i, j}^{(k)}}
$$
當 $k = 1$ 時,$z_j^{(1)} = \sum_{i} W_{i, j}^{(1)} x_i^{(n)}$,所以
$$
\frac{\partial z_j^{(1)}}{\partial W_{i, j}^{(1)}} = x_i^{(n)}
$$
當 $k > 1$ 時,$z_j^{(k)} = \sum_{i} W_{i, j}^{(k)} a_i^{(k-1)}$,所以
$$
\frac{\partial z_j^{(k)}}{\partial W_{i, j}^{(k)}} = a_i^{(k-1)}
$$
所以從輸入層開始,一層一層往前算,可以得到所有 $\frac{\partial z_j^{(k)}}{\partial W_{i, j}^{(k)}}$ 的值
Backward Pass
目標是計算第一項
$$
\frac{\partial c^{(n)}}{\partial z_j^{(k)}}
$$
不同 Cost function 會有不同的計算方式,以 Binary Classification 為例,當 $k = L$ 時,
$$
\begin{aligned}
\frac{\partial c^{(n)}}{\partial z_j^{(L)}} &= \frac{\partial}{\partial z_j^{(L)}} \text{softplus}(- (2y^{(n)} - 1) z^{(L)}) \newline
&= \sigma((1- 2y^{(n)}) z^{(L)}) (1-2y^{(n)}) \newline
\end{aligned}
$$
當 $k < L$ 時,
$$
\begin{aligned}
\frac{\partial c^{(n)}}{\partial z_j^{(k)}} &= \frac{\partial c^{(n)}}{\partial a_j^{(k)}} \cdot \frac{\partial a_j^{(k)}}{\partial z_j^{(k)}} = \frac{\partial c^{(n)}}{\partial a_j^{(k)}} \cdot \text{act}^{(k)\prime}(z_j^{(k)}) \newline
&= \left( \sum_{s} \frac{\partial c^{(n)}}{\partial z_s^{(k+1)}} \cdot \frac{\partial z_s^{(k+1)}}{\partial a_j^{(k)}} \right) \cdot \text{act}^{(k)\prime}(z_j^{(k)}) \newline
&= \left( \sum_{s} \frac{\partial c^{(n)}}{\partial z_s^{(k+1)}} \cdot \frac{\partial \sum_i W_{i, s}^{(k+1)}a_i^{(k)}}{\partial a_j^{(k)}} \right) \cdot \text{act}^{(k)\prime}(z_j^{(k)}) \newline
&= \left( \sum_{s} \frac{\partial c^{(n)}}{\partial z_s^{(k+1)}} W_{j, s}^{(k+1)} \right) \cdot \text{act}^{(k)\prime}(z_j^{(k)}) \newline
\end{aligned}
$$
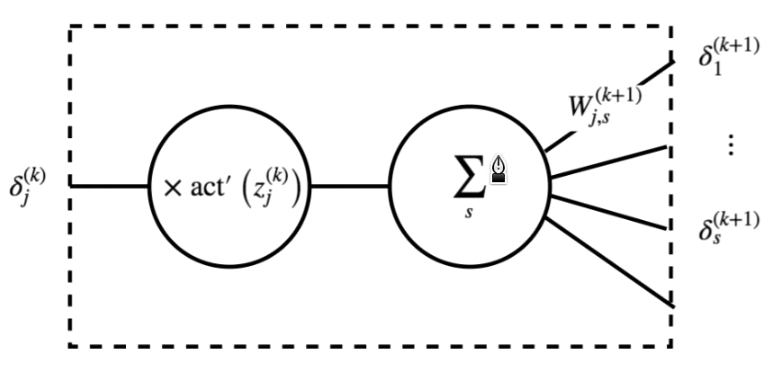
如果我們令 $\delta_j^{(k)} = \frac{\partial c^{(n)}}{\partial z_j^{(k)}}$,則可以寫成
$$
\delta_j^{(k)} = \left( \sum_{s} \delta_s^{(k+1)} W_{j, s}^{(k+1)} \right) \cdot \text{act}^{(k)\prime}(z_j^{(k)})
$$
可以發現,計算 $\delta_j^{(k)}$ 只需要用到下一層的 $\delta_s^{(k+1)}$,所以從輸出層開始,一層一層往後算,可以得到所有 $\frac{\partial c^{(n)}}{\partial z_j^{(k)}}$ 的值
Output Neuron Design
Sigmoid Units for Bernoulli Output Distributions
Sigmoid Output Unit:
$$
a^{(L)} = \hat \rho = \sigma(z^{(L)}) = \frac{e^{z^{(L)}}}{1 + e^{z^{(L)}}}
$$
$$
\delta^{(L)} = (1 - 2y^{(n)}) \sigma((1- 2y^{(n)}) z^{(L)})
$$
- 只有當 $z^{(L)}$ 很大或很小時,梯度才會消失,但那已經是正確分類了
Softmax Units for Categorical Output Distributions
$$
\delta_j^{(L)} = \frac{\partial c^{(n)}}{\partial z_j^{(L)}} = \frac{\partial - \log\hat P(y^{(n)} \mid x^{(n)};\Theta)}{\partial z_j^{(L)}} = \frac{\partial - \log (\prod_{i} \hat p_i^{\mathbb{1}(y^{(n)}=i)})}{\partial z_j^{(L)}}
$$
當 $j = y^{(n)}$ 時,
$$
\begin{aligned}
\delta_j^{(L)} &= -\frac{\partial \log \hat p_j}{\partial z_j^{(L)}} \newline
&= -\frac{\partial \log \frac{e^{z_j^{(L)}}}{\sum_{i} e^{z_i^{(L)}}}}{\partial z_j^{(L)}} \newline
&= - \frac{\partial (z_j^{(L)} - \log \sum_{i} e^{z_i^{(L)}})}{\partial z_j^{(L)}} \newline
&= - ( 1 - \frac{\partial \log \sum_{i} e^{z_i^{(L)}}}{\partial z_j^{(L)}} ) \newline
&= - ( 1 - \frac{e^{z_j^{(L)}}}{\sum_{i} e^{z_i^{(L)}}} ) \newline
&= \hat p_j - 1 \newline
\end{aligned}
$$
- 只有當 $\hat p_j$ 很接近 1 時,梯度才會消失,但那已經是正確分類了
當 $j \neq y^{(n)}$ 時,
$$
\begin{aligned}
\delta_j^{(L)} &= -\frac{\partial \log \hat p_i}{\partial z_j^{(L)}} \newline
&= -\frac{\partial \log \frac{e^{z_i^{(L)}}}{\sum_{k} e^{z_k^{(L)}}}}{\partial z_j^{(L)}} \newline
&= - \frac{\partial (z_i^{(L)} - \log \sum_{k} e^{z_k^{(L)}})}{\partial z_j^{(L)}} \newline
&= - ( 0 - \frac{\partial \log \sum_{k} e^{z_k^{(L)}}}{\partial z_j^{(L)}} ) \newline
&= - ( \frac{e^{z_j^{(L)}}}{\sum_{k} e^{z_k^{(L)}}} ) \newline
&= \hat p_j \newline
\end{aligned}
$$
- 只有當 $\hat p_j$ 很接近 0 時,梯度才會消失,但那已經是正確分類了
Hidden Neuron Design
Vanishing Gradient Problem
- 當使用 Sigmoid 或 Tanh 作為 Hidden Neuron 的 Activation Function 時,會遇到 Vanishing Gradient Problem,因為在算 $\delta$ 時,會有一個 Activation Function 的導數相乘,他們的值通常都小於 1,導致梯度越來越小,最後無法更新參數

所以 ReLU 被提出來解決這個問題,因為 ReLU 的導數在正區間是 1,不會導致梯度消失
- ReLU 也有一些缺點,例如在負區間導數為 0,可能會導致神經元死亡 (dying ReLU) 問題,但整體來說,ReLU 在深度神經網路中表現良好
- 其他的 Activation Function 例如 Leaky ReLU、ELU、GELU 也被提出來解決 ReLU 的缺點,並且在某些情況下表現更好
Maxout Units
$$
f_j^{(k)} = \max_{i=1}^{m} (W_{:, (j-1)m + i}^{(k)\top} a^{(k-1)} + b_{(j-1)m + i}^{(k)})
$$
- Maxout Units 可以看作是多個線性函數的最大值,能夠學習更複雜的非線性函數
- Maxout Units 也能夠減少 Vanishing Gradient Problem,因為它的梯度不會消失
- 但 Maxout Units 需要更多的參數,可能會導致過擬合 (overfitting) 問題
Neural Networks: Optimization
- Non-Convexity
- 實際上 Local Minima 數量非常少,不太會卡在 Local Minima
- 很多 NN 缺乏 Global Minimum
- Training 101
- 先針對每個 Feature z-normalization
- 把所有 Weights 初始化成小的隨機值 (e.g. Xavier Initialization, He Initialization)
- 把 Bias 初始化成 0 (如果是 ReLU 的話,可以初始化成小的正值)
- Early Stopping
- 監控 Validation Loss,如果 Validation Loss 開始上升,表示模型開始 Overfit,可以停止訓練
Momentum
改用 $v^{(t)}$ 來累積過去的梯度資訊,可以避免卡在局部震盪區域
$$
v^{(t+1)} \leftarrow \lambda v^{(t)} - (1-\lambda) g^{(t)} \newline
\Theta^{(t+1)} \leftarrow \Theta^{(t)} + \eta v^{(t+1)}
$$
Nesterov Momentum
會用 Lookahead 的方式來計算梯度
$$
~\Theta^{(t+1)} \leftarrow \Theta^{(t)} + \eta v^{(t)} \newline
v^{(t+1)} \leftarrow \lambda v^{(t)} - (1-\lambda) \nabla_{\Theta} C(~\Theta^{(t+1)}) \newline
\Theta^{(t+1)} \leftarrow \Theta^{(t)} + \eta v^{(t+1)}
$$
- Nesterov Momentum 可以更快地收斂,因為它考慮了未來的梯度方向
- 對缺乏 Minima 的問題沒幫助
Adaptive SGD
可以動態調整 Learning Rate,讓收斂更快,且不同方向可以有不同的 Learning Rate
AdaGrad
$$
r^{(t+1)} \leftarrow r^{(t)} + g^{(t)} \odot g^{(t)} \newline
\Theta^{(t+1)} \leftarrow \Theta^{(t)} - \eta \frac{g^{(t)}}{\sqrt{r^{(t+1)}} + \epsilon}
$$
$$
\frac{\eta}{\sqrt{r^{(t+1)}}} = \frac{\eta}{\sqrt{t+1}} \odot \frac{1}{\sqrt{\frac{1}{t+1} \sum_{\tau=0}^{t} g^{(\tau)} \odot g^{(\tau)}}}
$$
- AdaGrad 會讓 Learning Rate 隨著時間減小
- 某方向的梯度如果很大,則該方向的 Learning Rate 會變小
但是同一個方向的 Learning Rate 會從一開始就一直累積,我們應該只要拿最近的梯度來調整 Learning Rate 就好
RMSProp
$$
r^{(t+1)} \leftarrow \lambda r^{(t)} + (1-\lambda) g^{(t)} \odot g^{(t)} \newline
\Theta^{(t+1)} \leftarrow \Theta^{(t)} - \eta \frac{g^{(t)}}{\sqrt{r^{(t+1)}} + \epsilon}
$$
- RMSProp 只會考慮最近的梯度資訊,能夠更快地適應新的梯度方向
Adam
結合了 Momentum 和 RMSProp 的優點
$$
v^{(t+1)} \leftarrow \lambda_1 v^{(t)} + (1-\lambda_1) g^{(t)} \newline
r^{(t+1)} \leftarrow \lambda_2 r^{(t)} + (1-\lambda_2) g^{(t)} \odot g^{(t)} \newline
\Theta^{(t+1)} \leftarrow \Theta^{(t)} - \eta \frac{v^{(t+1)}}{\sqrt{r^{(t+1)}} + \epsilon}
$$
Batch Normalization
越深的 NN 越容易受到 ill-conditioning 的影響,因為每一層的 $W$ 都會互相影響,導致訓練不穩定
當我們計算第 $i$ 個參數的梯度 $g_i^{(t)} = \frac{\partial C}{\partial w^{(i)}}$ 時:
- 偏微分 (Partial Derivative)。
- 我們假設只有 $w^{(i)}$ 在變動,而其他的維度 $w^{(j)}$ ($j \neq i$) 都是固定不變的。
當我們執行 $\Theta^{(t+1)} \leftarrow \Theta^{(t)} - \eta g^{(t)}$ 時:
- 實際行為:所有的參數 $w^{(1)}, \dots, w^{(L)}$ 在同一個 iteration 中同時改變了數值。
- 造成的後果:原本 $w^{(i)}$ 預期「其他人都固定」的前提被打破了。
我們以為:只要每個參數 $\Theta_i$ 都往它自己認為「好」的方向走,整體誤差 $C$ 就會下降。
- 線性情況:如果 $C$ 是線性的,這個假設成立。
- **非線性情況 (深度學習)**:參數之間通常高度相關 (Correlated)。當所有參數同時移動,可能會產生干擾,導致 $C(\Theta^{(t+1)})$ 不降反升,或者在峽谷壁上來回震盪 (Zig-zag),收斂極慢。
Batch Normalization 的目標是讓每一層的輸入分布穩定,減少參數之間的干擾
$$
\begin{aligned}
\mu_B &= \frac{1}{m} \sum_{i=1}^{m} a_i^{(k)} \newline
\sigma_B^2 &= \frac{1}{m} \sum_{i=1}^{m} (a_i^{(k)} - \mu_B)^2 \newline
~{a}_i^{(k)} &= \frac{a_i^{(k)} - \mu_B}{\sigma_B} \newline
\end{aligned}
$$
- $M$: mini-batch 大小
- $a_i^{(k)}$: 第 $k$ 層第 $i$ 個神經元的輸出
- $\gamma^{(k-1)}, \beta^{(k-1)}$: learnable parameters,可以讓模型學習到適合的輸入分布
在 Testing 時,會使用整個 Training Set 的平均和方差來做 Normalization
一般來說,Activation Function 是 Non-Linear 的,所以 Batch Normalization 通常會放在 Activation Function 之前
$$
\begin{aligned}
\mu_B &= \frac{1}{m} \sum_{i=1}^{m} z_i^{(k)} \newline
\sigma_B^2 &= \frac{1}{m} \sum_{i=1}^{m} (z_i^{(k)} - \mu_B)^2 \newline
~{z}_i^{(k)} &= \frac{z_i^{(k)} - \mu_B}{\sigma_B} \newline
a_i^{(k)} &= \text{act}^{(k)}(\gamma^{(k)} ~{z}_i^{(k)} + \beta^{(k)}) \newline
\end{aligned}
$$
$~{z}_i^{(k)}$ 如果是 zero mean, unit variance 的話,經過 Activation Function 後,可能會降低模型的 Expressiveness,所以引入了 $\gamma^{(k-1)}, \beta^{(k-1)}$ 來讓模型學習到適合的輸入分布
Curriculum Learning
模型權重的初始化非常重要,可能會決定模型最後的表現
Continuation Methods
先把模型簡化,讓模型容易訓練,然後慢慢增加模型的複雜度
$$
~C(\Theta) = E_{~\Theta \sim \mathcal{N}(\Theta, \sigma^2)} C(~\Theta)
$$
每次計算 Cost 時,會去取 $\Theta$ 附近的參數 $~\Theta$ 來計算 Cost 的平均,讓整體 Cost 變得比較平滑,這樣 Gradient Descent 會更好解,解完之後再代回去解更難的問題
- 問題
- Cost Function 可能不是 Convex
- 無法解沒有 minima 的問題
Curriculum Design
先提高簡單樣本的權重,讓模型先學會簡單樣本,然後慢慢增加困難樣本的權重
就像是人類學習一樣,先從簡單的東西開始學,然後再學複雜的東西
Regularization
就算你有很大量的資料,還是會需要 Regularization,因為有些任務 (images, audio, text) 的困難度是無上限的,所以模型還是有可能 Overfit
對於簡單問題來說,可以讓問題更 well defined
Weight Decay
通常會用 column norms $\Omega(W_{:, j}^{(k)})$ 來做正則化
- 可以避免 weights 和 $z_j^{(k)}$ 過大
Explicit Weight Decay
$$
\argmin_\Theta C(\Theta) \text{subject to} \Omega(\Theta) \leq R
$$
搭配 Projective SGD 來解這個問題,每次算出 $\Theta^{(t+1)}$ 後,會把 $\Theta^{(t+1)}$ 投影到 $\Omega(\Theta) \leq R$ 的範圍內
- 可以避免 Dead Units 問題,因為沒有限制 weights 一定要接近 0
- 在 Learning rate 太大的時候,也不會有問題,因為 weights 會被投影回去
Hinton 建議可以採用 explicit constraint + reprojection + large learning rate 的方式來訓練 NN
Data Augmentation
對於圖片資料來說,除了可以做 Flip, Rotation, Crop, Scale 等等的變換外,還可以加入 Noise Injection ,讓 function $f$ locally constant,讓模型對於輸入的微小變化不敏感,增加模型的泛化能力
Dropout
Ensemble Method
- Voting: 對多個模型的預測結果做投票,選出最多票的結果作為最終預測
- Bagging: 對多個模型的預測結果做平均,作為最終預測
Dropout 是一種在訓練過程中隨機丟棄神經元的技術,可以看作是一種 Bagging 的方法
- 0.8 for input layer
- 0.5 for hidden layer
在預測時,有兩種方式:
- Mask Sampling: Sample 多個 Mask,對每個 Mask 的預測結果做平均
- Weight Scaling: 把每個神經元的輸出乘上保留的機率 (e.g. 0.5),這樣可以近似所有 Mask 的平均效果
Manifold Regularization
Manifold 意思是資料分布在高維空間中的低維結構,所以我們希望模型在這些低維結構上是平滑的
Tangent Propagation
- Tangent Vectors: 描述資料在 Manifold 上的變化方向
- Tangent Propagation: 在訓練過程中,加入對 Tangent Vectors 的正則化,讓模型在這些方向上是平滑的
Domain-Specific Model Design
Word2Vec: weight tying
- weight tying 是指在模型中,共用某些參數,這樣可以減少參數的數量,並且讓模型更容易學習到有用的特徵
CNN: convolution + pooling
- convolution 可以讓模型學習到局部的特徵,並且具有平移不變性
- pooling 可以減少特徵的維度,並且讓模型更具有平移不變性
Convolutional Neural Networks
- Image-Specific Priors
- 人臉不管怎麼平移,都是人臉,是 location independent 的
- Pruned Connections
- Fully Connected Layer: 每個神經元都和前一層的所有神經元相連
- Convolutional Layer: 每個神經元只和前一層的部分神經元相連,這樣可以減少參數的數量,並且讓模型更容易學習到局部的特徵
- Patterns 可以 Zoom in/out
- Pooling Layer: 可以讓模型學習到不同尺度的特徵,還可以減少特徵的維度
- Tied Weights
- Convolutional Layer: 同一個 Filter 在整個輸入圖像上滑動,這樣可以減少參數的數量
Filters and Feature Maps
在地 $l$ 層的第 $i$ 個 Neuron 的輸出為:
$$
a_i^{(l)} = \text{act}^{(l)}([a_{i-K/2}^{(l-1)}, \ldots, a_i^{(l-1)}, \ldots, a_{i+K/2}^{(l-1)}]^\top \cdot W^{(l)} + b^{(l)})
$$
其中 $[W_1, \ldots, W_K]$ 用來給同一個 Group 的 Neurons 使用,稱為 Filter 或 Kernel
一組 Neurons 的輸出稱為 Feature Map
深層 filter
- 可以看到上一層同個區域的所有 Patterns
- 可以看到更大的 receptive field,能夠學習到更高階的特徵
Pooling Layer
- Max Pooling: 取區域內的最大值,更好偵測 edges、textures,判斷有無某個特徵存在
- Average Pooling: 取區域內的平均值,更好偵測 brightness、contrast,判斷整體特徵的強度
- 可以減少特徵的維度
Equivariance and Invariance
Convolutional Layer: Equivariant to Translation
- 如果輸入圖像平移,輸出特徵圖也會平移
Max Pooling Layer: Invariant to Small Translations
- 如果輸入圖像平移,輸出特徵圖不會改變
- 不適合 segmentation、object detection 等需要精確位置的任務
CNN Variants
- Dilation
- 跳過一些像素來做 convolution,可以增加 receptive field 的大小
- Cross-Filter Feature Pooling
- 在同一層的不同 Filter 之間做 Pooling,可以增加特徵的多樣性
- Channel Grouping
- 第二層的 Filter 只看第一層的部分 Feature Maps,可以減少參數的數量
Case Studies
LeNet-5
- 手寫數字辨識
- 使用兩層 Convolutional Layer 和兩層 Fully Connected Layer
AlexNet
- ImageNet 2012 冠軍
- 使用 ReLU 作為 Activation Function
- dropout 來減少 Overfitting
- GPU 加速訓練
VGG
- Filter Size: 3x3,非常小
- Network Depth: 非常深,達到 19 層
GoogLeNet (Inception)
- Inception Module: 同一層使用多種不同大小的 Filter,然後把結果串接起來
- Bottleneck Layers: 使用 1x1 的 Filter 來減少特徵的維度,減少計算量
ResNet
- Residual Connections: 讓訊息可以直接從前一層傳到後面幾層
- 可以訓練非常深的網路,達到 152 層
- FCN: Fully Convolutional Network
- 把 Fully Connected Layer 換成 Convolutional Layer,可以處理任意大小的輸入圖像
DenseNet
- Dense Connections: 每一層都和前面所有層相連
Recurrent Neural Networks
Sequential Data
- Letters in words
- Words in sentences
- Phonemes in speech
- Frames in video
Dataset: $\mathbf{X} = { (x^{(n, t)}, y^{(n, t)})}_t \in \mathbf{R}^{N \times (D, K) \times T}$
- $T$ 稱為 horizon,表示序列的長度
$$
a^{(k, t)} = \text{act}^{(k)}(W^{(k)} a^{(k-1, t)} + U^{(k)} a^{(k, t-1)})
$$
- $W^{(k)}$ 和 $U^{(k)}$ 不會隨時間改變,是 Shared Weights
Variants of RNNs
- One2Many: e.g. Image Captioning
- Many2One: e.g. Sentiment Analysis
- Many2Many:
- (Synced): e.g. Video Keyframe Tagging
- (Unsynced): e.g. Machine Translation
BiDirectional RNNs
- 可以同時考慮過去和未來的資訊
$$
a^{(k, t)} = \text{act}^{(k)}(W^{(k)} a^{(k-1, t)} + U^{(k)} a^{(k, t-1)}) \newline
\bar{a}^{(k, t)} = \text{act}^{(k)}(\bar{W}^{(k)} a^{(k-1, t)} + \bar{U}^{(k)} \bar{a}^{(k, t+1)}) \newline
$$
Recursive RNNs
- 用在樹狀結構的資料,例如句法分析樹
$$
a^{(k, t)} = \text{act}^{(k)}(W^{(k)} a^{(k-1, \text{left}(t))} + U^{(k)} a^{(k-1, \text{right}(t))})
$$
Training RNNs
Cost Function
$$
\begin{aligned}
\argmin_{\Theta} C(\Theta) &= \argmin_{\Theta} -\log P(\mathbf{X} | \Theta) \newline
&= \argmin_{\Theta} -\sum_{n, t} \log P(y^{(n, t)} \mid x^{(n, t)}, \ldots, x^{(n, 1)}, \Theta) \newline
&= \argmin_{\Theta} \sum_{n, t} C^{(n, t)}(\Theta) \newline
\end{aligned}
$$
Binary Classification
假設 $P(y^{(n, t)} = 1 \mid x^{(n, t)}, \ldots, x^{(n, 1)}) \sim \text{Bernoulli}(\rho^{(t)})$,則
$$
C^{(n, t)}(\Theta) = (a^{(L, t)})^{y^{(n, t)}} (1 - a^{(L, t)})^{1-y^{(n, t)}}
$$
SGD-based Training
$$
\Theta^{(t+1)} \leftarrow \Theta^{(t)} - \eta \nabla_{\Theta} \sum_{n, t} C^{(n, t)}(\Theta^{(t)})
$$
令 $c^{(n, t)} = C^{(n, t)}(\Theta^{(t)})$,則需要計算所有 $i, j, k, n, t$ 的偏微分
$$
\frac{\partial c^{(n, t)}}{\partial W_{i, j}^{(k)}}, \quad \frac{\partial c^{(n, t)}}{\partial U_{i, j}^{(k)}}
$$
$\frac{\partial c^{(n, t)}}{\partial W_{i, j}^{(k)}}$ 跟之前類似,這邊只 focus 在 $\frac{\partial c^{(n, t)}}{\partial U_{i, j}^{(k)}}$ 上
$$
\frac{\partial c^{(n, t)}}{\partial U_{i, j}^{(k)}} = \frac{\partial c^{(n, t)}}{\partial z_j^{(k, t)}} \frac{\partial z_j^{(k, t)}}{\partial U_{i, j}^{(k)}}
$$
Forward Pass
目標是計算第二項
$$
\frac{\partial z_j^{(k, t)}}{\partial U_{i, j}^{(k)}}
$$
$z_j^{(k, t)} = \sum_{i} W_{i, j}^{(k)} a_i^{(k-1, t)} + \sum_{i} U_{i, j}^{(k)} a_i^{(k, t-1)}$,所以
$$
\frac{\partial z_j^{(k, t)}}{\partial U_{i, j}^{(k)}} = a_i^{(k, t-1)}
$$
Backward Pass
目標是計算第一項
$$
\frac{\partial c^{(n, t)}}{\partial z_j^{(k, t)}}
$$
$$
\begin{aligned}
\frac{\partial c^{(n, t)}}{\partial z_j^{(k, t)}} &= \frac{\partial c^{(n, t)}}{\partial a_j^{(k, t)}} \cdot \frac{\partial a_j^{(k, t)}}{\partial z_j^{(k, t)}} \newline
&= \frac{\partial c^{(n, t)}}{\partial a_j^{(k, t)}} \cdot \text{act}^{(L)\prime}(z_j^{(k, t)}) \newline
&= (\sum_s \frac{\partial c^{(n, t)}}{\partial z_s^{(k, t+1)}} \cdot \frac{\partial z_s^{(k, t+1)}}{\partial a_j^{(k, t)}} + \sum_s \frac{\partial c^{(n, t)}}{\partial z_s^{(k+1, t)}} \cdot \frac{\partial z_s^{(k+1, t)}}{\partial a_j^{(k, t)}}) \cdot \text{act}^{(k)\prime}(z_j^{(k, t)}) \newline
\end{aligned}
$$
所以可以寫成
$$
\delta_j^{(k, t)} = \left( \sum_{s} \delta_s^{(k, t+1)} U_{j, s}^{(k)} + \sum_{s} \delta_s^{(k+1, t)} W_{j, s}^{(k+1)} \right) \cdot \text{act}^{(k)\prime}(z_j^{(k, t)})
$$
BPTT Through Time (BPTT)
Single forward pass + Multiple backward passes
Optimization
RNN 的 neuron 有 Long-Term Dependencies 的問題,會導致梯度消失或爆炸,可以用以下方法解決:
- Nesterov Momentum: 可以加速收斂,減少震盪
- Gradient Clipping: 當梯度過大時,將梯度縮放到一個合理的範圍內
- RMSProp / Adam: 使用自適應學習率的方法來更新參數
Optimization-Friendly Model
Sigmoid / Tanh
可以避免梯度爆炸的問題,但會有梯度消失的問題
LSTM
引入了記憶單元 (Cell State) 和門控機制 (Gates),可以有效地解決梯度消失和爆炸的問題
- Memory Cell: 負責儲存長期的資訊
- Forget Gate: 控制要忘記多少過去的資訊 (0~1)
- Input Gate: 控制要加入多少新的資訊到 Memory Cell (0~1)
- Output Gate: 控制要輸出多少資訊到下一層 (0~1)
Teacher Forcing
在訓練過程中,使用真實的輸出作為下一個時間步的輸入,這樣每個時間點可以平行訓練,不需要等到前一個時間點的輸出出來才能訓練下一個時間點
但可能會減少模型的 Expressiveness,因為模型沒有學會自己產生輸出
Augmented RNNs
Attention Mechanism
- 可以讓模型在每個時間點都能夠關注到輸入序列的不同部分